Scheme language

I’ve been reading SICP (Structure and Interpretation of Computer Programs) recently, and I feel that I’ve benefited a lot from it, so I’m going to summarize and share some of what I’ve learned.SICP is very comprehensive, and the content includes functional programming, hierarchical and abstraction of data structures, object-oriented, infinite streams, meta-cyclic interpreters, inert value, non-deterministic programming, logic programming, assembly language and machines, compilation principles, and more. The theme of this series of articles is continuation, and the main topics may include:

Scheme language
Scheme meta loop interpreter
The magic of `call/cc'.
call/cc via the CPS interpreter.
call/cc via CPS transforms.
…

I’ve been reading the last chapter recently and will see about updating some of the content when I finish the book. The basis of this content is the Scheme language, so we’ll start with an introduction to the Scheme language. The main purpose of this article is to let people who don’t know anything about Scheme understand the next few articles, so we won’t get into the details. If you want to know more about it, you can read the relevant documentation.

1 Characteristics of Scheme

Scheme is a dialect of Lisp. Lisp is the second oldest language in the world (Fortran being the first) and has many dialects. These dialects share a common feature - they are based on S-expressions.

S-expressions can be atomic expressions (atom) or lists. Atomic expressions can be numbers, such as 1 , 42 , 3.14; strings, such as "hello"; booleans, such as #t , #f; or just symbols, such as a , if , add. A list, on the other hand, is a number of S-expressions in a pair of parentheses, separated by spaces:

`1`	`(<s-exp1> <s-exp2> <s-exp3> ...)`

Some examples of S-expressions are given below:

100
100.13
"Hello world"
(add 1 2)
(display "Hello world")
(list (list 1 2) (list "a" "b"))

The first three S-expressions are atomic expressions. (add 1 2) is a list of length 3, where the three elements are the symbol add, the number 1, and the number 2. (display "Hello world") is a list of length 2, where the first element is the symbol display, and the second element is the string "Hello world". (list (list 1 2) (list "a" "b")) is a list of length 3, the three elements are the symbol list, list (list 1 2), and list (list "a" "b").

Scheme is composed entirely of S-expressions. In Scheme, the first element of a compound expression is used as the type of the expression, and the remaining elements are used as the parameters of the expression.

S-expressions

The type of the expression determines the semantics of the expression and the meaning of its arguments. For example, an if expression takes three arguments, the first of which is a condition, the second of which is an expression that is executed when the condition is true, and the third of which is an expression that is executed when the condition is false. Since S-expressions can be nested arbitrarily, they can be used to construct arbitrarily complex code. The following is an example of Scheme code:

(define (queens board-size)
  (define (queen-cols k)
    (if (= k 0)
      (list '())
      (filter
        (lambda (positions) (safe? positions))
        (flatmap
          (lambda (rest-of-queens)
            (map (lambda (new-row)
                   (adjoin-position new-row k rest-of-queens))
                 (enumerate-interval 1 board-size)))
          (queen-cols (- k 1))))))
  (queen-cols board-size))

You can see that S-expressions are nested in layers, forming a tree structure, which is actually the syntax tree. This means that the language actually writes out the syntax tree explicitly. Later we can see the benefits of this approach: the code can be directly represented as a data structure, and the code is extremely easy to parse and compile.

2 Programming Environment

Scheme, as a dialect of Lisp, has many dialects of its own, such as Chez Scheme, MIT Scheme, Racket, and so on. The environment we use is Racket, which is powerful and easy to use. We can download the latest version from its official website. Racket comes with an IDE called DrRacket, which we can use to learn to write Scheme.

Open DrRacket and you are ready to start Scheme programming. The first line of the program should declare the language #lang racket. Once you have edited the program, click “Run” to execute the code.

DrRacket

Some people may not be used to a language that is full of parentheses, and it is cumbersome to read code that requires counting parentheses. But if the code is properly indented and aligned, the nesting relationships are readily apparent. We can make the parameters on a separate line and indent them by two spaces relative to the type:

(type
  arg1
  arg2
  ...)

Or the first argument is placed on the same line as the type, and subsequent arguments are aligned with the first argument:

1
2
3

(type arg1
      arg2
      ...)

If the first parameter is special, you can also have the first parameter on the same line as the type, with the remaining parameters on a separate line and indented by two spaces.

(type special-arg1
  arg2
  arg3
  ...)

These are basically the three indentation styles. With DrRacket, indentation is automatic; you don’t need to worry about parentheses when reading code, you can just look at the code indentation, just like Python.

3 Basic Expressions

A high-level language must have these three elements:

primitive expressions: the simplest, most basic elements that a language provides.
methods of combination: methods for combining atomic expressions into composite elements.
methods of abstraction: naming composite elements so that they can be manipulated as a whole.

We say assembly language is not a high-level language because it has very weak combinatorial and abstraction capabilities. For example, add $42 %eax can represent eax + 42, but to represent (eax + 42) * 3, you have to write two instructions, because the language has no ability to nest combinations. As for abstraction, the function in assembly (subroutine, to be precise) is more like a goto, whereas Scheme is a very high-level language because it has very strong combinatorial and abstraction capabilities, as we’ll see later.

3.1 Atomic expressions

There are so many kinds of atomic expressions:

Numbers. Can be integers 10, -12; floating point numbers 3.14; rational numbers 1/2, -3/5, in the form of two integers separated by /, taking care that there is no space in between, as this is an atom.
String. Identified by double quotes, such as "Hello world".
Boolean. There are two types, #t and #f.
Symbol. Also known as “variables”, or identifiers. For example, pi, with a value of 3.141592653589793; sqrt, a built-in function. Unlike many languages, Scheme’s symbols are not limited to letters, numbers, and underscores; for example, reset!, *important*, +, and 1st-item are all valid symbols.

3.2 Compound Expressions

There are two types of compound expressions in Scheme, special forms and function calls.The syntax for Scheme function calls is (function arg1 arg2 ...). Let the first element of an S-expression be a function. The remaining elements are function arguments. For example, the following expressions are function calls:

1
2
3

(sqrt 2)
(+ 1 2)
(* (+ 1 2) (+ 3 4))

Here sqrt, +, and * are function names that perform square root, addition, and multiplication operations, respectively. Unlike most other languages, Scheme has no operators; addition, subtraction, multiplication, division, comparison, etc. are all functions.

It may seem strange to beginners, but this syntax has great benefits. First of all, the relationship between expressions is clear and unambiguous, so the programmer does not need to remember the priority of operators, whether to combine left or right, and the program is easy to parse and compile. The usage is uniform, unlike C, where multiplication is a * b and exponentiation is pow(a, b). You don’t need the complex operator overloading rules of C++, you can just define a function named +, *.

Some common functions and calls are given below:

(+ 1 1) ;; Addition
(- 1 1) ;; subtraction
(* 2 3) ;; multiplication
(/ 3 2) ;; Division. Integer division returns rational numbers; this example returns 3/2
(= 2 2) ;; Determine if two numbers are equal
(< 2 3) ;; Whether the first argument is smaller than the second. Similarly >, <= >=
(eq? a b) ;; Determining whether two objects are the same can be interpreted as comparing addresses
(remainder 3 2) ;; Remainder. This example returns 1
(sqrt 2) ;; sqrt
(display "Hello world") ;; Print to standard output
(newline) ;; Print line breaks

The semicolon ; is used as a one-line comment in Scheme.

Looking at this, you might think that the expression (if (> a b) a b) is also a call to an if function. But it’s not. When you evaluate a function, you evaluate each argument in turn, and then you call the function. In the case of if, when (> a b) is true, only a should be evaluated, not b. Conversely, only b should be evaluated. Therefore if cannot be a function, it should be a special form.

S An expression is like a representation of a syntax tree, and a special form is a particular syntax that defines which child nodes the syntax has and what they mean. Some common special forms and how to use them are given below.

(if predicate consequence alternative) ;; Returns consequence if predicate is true, alternative otherwise.

;; Square brackets [] are equivalent to parentheses () and can be interleaved to improve readability.
(cond [predicate1 consequence1] ;; In order: if predicate1 is true return consequence1
      [predicate2 consequence2] ;; Returns consequence2 if predicate2 is true.
      ...
      [else alternative]) ;; If all the conditions do not hold, return alternative

(define var val) ;; Define the value of the variable var as val

(and exp1 exp2 ...) ;; Logic and, following the short-circuit principle (so it must be a special form)
(or exp1 exp2 ...) ;; Logical or, following the short-circuit principle
;; Logical not, a function (not exp)

(begin exp1 exp2 ...) ;; In sequential order, exp1, exp2, ... The value of the whole expression is the value of the last expression. Similar to the comma operator in C.

(lambda (arg1 arg2 ...) body ...) ;; Constructing a function, described in detail in Section 4

4 Defining functions

The lambda special form creates a function of the form (lambda (arg1 arg2 ...) body ...). where (arg1 arg2 ...) is the argument list, and the remaining body ... is the body of the function, which can consist of multiple expressions, and the return value of the function is the value of the last expression. Functions are usually defined in conjunction with define, an example of which is given below.

(define gcd
  (lambda (a b)
    (if (= b 0)
        a
        (gcd b (remainder a b)))))

This function implements Euclid’s algorithm to find the greatest common divisor of two integers a and b. The argument list is (a b), and the body of the function consists of a single if expression. The if expression checks if b is 0 and returns a if b is 0, otherwise it recursively calls itself (gcd b (remainder a b)). Now we can call gcd:

1
2

(gcd 10 12) ;; 2
(gcd 7 11) ;; 1

4.1 Environment

Functions can be nested. For example, to define the function prime? to determine whether a number is prime, we look for an integer greater than 1 that divides it. If we can’t find an integer that divides it, then it is a prime number.

(define (prime? n)
  (define (iter i)
    (cond [(> (* i i) n) #t]
          [(= (remainder n i) 0) #f]
          [else (iter (+ i 1))]))
  (iter 2))

The environment in which prime? is located is called the global environment, and the environment in which iter is located is the internal environment of prime?. When define is executed, it adds a variable to the environment it is in. When a function is called, a new environment is created that inherits the environment in which the function was defined; the function’s arguments are instantiated in the new environment. To find the value of an expression, the value of the variable is looked for in the current environment, and if it is not found, it is looked for in the higher environment, and so on. Thus to examine the behavior of a function, two elements must be considered: the code for the function, and the environment in which the function resides. Together, these two elements are sometimes called “c”.

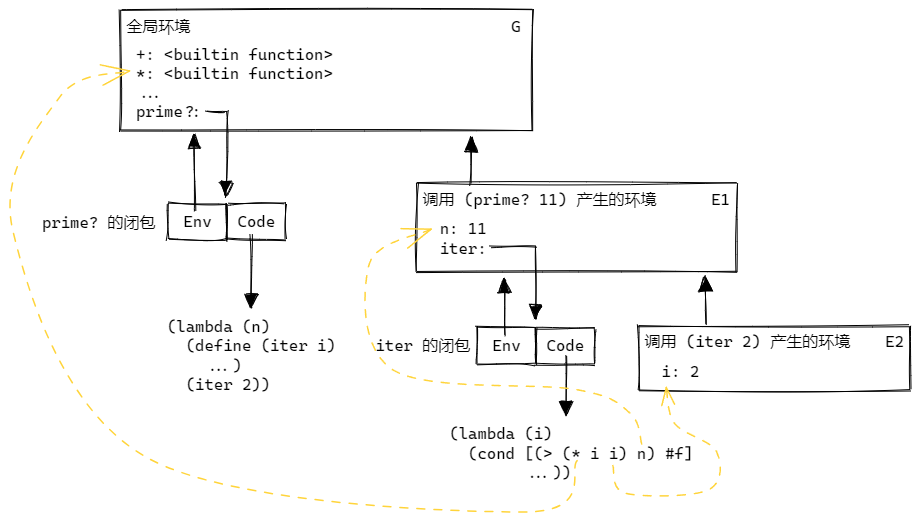
scheme lang https://cdn.jsdelivr.net/gh/b0xt/sobyte-images1/2023/07/13/4a114b9f3f7342ee9553208d94fb9298.png

When we execute (prime? 11) in the global environment, there are these steps:

Find the prime? variable in the global environment, discover that it is a function, call it.
Read the Env field of the closure and find that the environment of this this function is the global environment G, so create a new environment that inherits G, denoted E1.
Instantiate the arguments in E1 with n: 11.
Start executing the code for prime?.
Execute (define (iter i) ...), adding the variable iter to E1. iter is a function in an environment pointing to E1.
Execute (iter 2), find iter in E1, find that it is a function, call it.
Finds that the environment of this function is E1, so creates a new environment that inherits from E1, denoted E2.
Instantiate arguments in E2 with i: 2.
Start executing the code for iter.
Executed to (> (* i i) n):
- Looked for variable * in E2 and couldn’t find it; then looked again in E1 and still couldn’t find it; finally found * as a built-in function in G.
- Looked for variable i in E2 and found i: 2.
- Looked for variable n in E2, couldn’t find it; then looked in E1, found n: 11
- …
…
Execute (iter (+ i 1)) to find i: 2 in E2 and iter in E1. Call iter.
Finds that iter is in environment E1, so creates a new environment E3 that inherits from E1.
Instantiate parameters in E3 with i: 3.
Start executing the code for iter, and so on.

This is how the Scheme environment works. In the next article we will implement this mechanism to realize a Scheme interpreter.

Scheme functions are first class citizens and can be passed as arguments or returned as values. When a function is passed, its environment is also passed. Example:

(define (f x)
  (lambda () x))

(define n (f 10))
(n) ;; 10

The f function returns a function that holds the environment created when f was called. So we can use this function to get the values passed in when f was called. We’ll see an interesting application of this mechanism later.

4.2 `let` and `let*`

When we need an intermediate variable, e.g. to calculate $5(3x^2+1)^2 + 4(3x^2+1)$, we need an intermediate variable $t=3x^2+1$ in order to avoid double-counting, and we will use the let special form for this purpose.

1
2

(let ([t (+ (* 3 x x) 1)])
  (+ (* 5 t t) (* 4 t)))

The syntax of let has the following format:

(let ([var1 val1] ;; Define several variables
      [var2 val2]
      ...)
  body            ;; These variables can be used in body
  ...)
;; These variables cannot be used outside of let

It’s really a syntactic sugar, which is equivalent to creating a function using lambda and then calling it immediately:

((lambda (var1 var2 ...)
    body
    ...)
  val1 val2 ...)

let has the drawback that you can’t define the value of a later variable in a way that references the earlier variable, i.e. (let ([a 1] [b (+ a 1)]) b) is illegal. So we have let*:

(let* ([var1 val1]
       [var2 val2] ;; val2 can refer to var1
       ...)
  body
  ...)

It is also a syntactic sugar, equivalently:

(let ([var1 val1])
  (let ([var2 val2])
    (let ...
      body
      ...))

let* is implemented by nesting lets, thus allowing references to preceding variables.

5 Data Structures

While the previous section covered combining and abstracting code, this section covers data structures. This series of articles will only use very simple data structures.

5.1 Ordered pairs and lists

To construct a composite structure, we use cons to construct ordered pairs (pairs). car gets the first element of the ordered pair and cdr gets the second element of the ordered pair.

1
2
3

(define p (cons 1 2))
(car p) ;; 1
(cdr p) ;; 2

Ordered pairs can be arbitrarily nested, as in (cons (cons 1 2) (cons 3 4)). Because they can be arbitrarily nested, it is theoretically possible to construct arbitrarily complex data structures from ordered pairs alone. If the ordered pairs are concatenated sequentially, a linked list is obtained:

`1`	`(cons 1 (cons 2 (cons 3 (cons 4 '()))))`

Thus for lists, car is used to get the first element of the list, cdr is used to get the remaining elements of the list, and cons inserts an element at the head of the list.

(define items (list 1 2 3 4))

(car items) ;; 1
(cdr items) ;; '(2 3 4)
(cons 0 items) ;; '(0 1 2 3 4)

(car (cdr items)) ;; 2
(car (cdr (cdr items))) ;; 3
(cdr (cdr (cdr items))) ;; '(4)
(cdr (cdr (cdr (cdr items)))) ;; '()

5.2 Quote

You may be wondering what the single quotes ' in '() and '(2 3 4) mean. Recall from Section 1 that S-expressions can be atomic expressions or lists. Yes, the list we’re talking about here is the same thing as the list created by the list function. That is, the S expression (1 2 3 4) is itself a list. But this expression is interpreted by Scheme as a call to function 1, passing in arguments 2, 3, 4. To represent the list itself, we use the quote special form. quote takes an S-expression as an argument, and instead of evaluating the expression, it returns it. Here are some examples of its use.

(quote (1 2 3 4)) ;; Equivalent to (list 1 2 3 4)
(quote a) ;; Instead of considering a to be a variable, it returns the symbol a itself.
(quote (+ a b)) ;; Returns a list of length 3, with the symbol +, the symbol a, and the symbol b as the three elements.
(quote (lambda (x) (* x x))) ;; Any code can be put into the quote

Since quote is so common, we have a simplified form. Preceding any S-expression with single quotes ' means quote the S-expression.

'a ;; Equivalent to (quote a)
'() ;; is equivalent to (quote ()), which represents an empty list, also known as NIL
'(1 2 3 4) ;; Equivalent to (list 1 2 3 4)
'(lambda (x) (* x x)) ;; Any code can be preceded by single quotes to indicate that the code itself

This is very important - it means that code can be parsed as data. This is a capability not available in other non-Lisp-based languages. We’ll be using it a lot in the next article, so let’s look at some simple examples first:

(define code '(lambda (x) (* x x)))

(car code) ;; 'lambda
(cadr code) ;; '(x)
(caddr code) ;; '(* x x)

Here cadr and caddr are shortcut functions. (cadr x) is equivalent to (car (cdr x)), and (caddr x) is equivalent to (car (cdr (cdr x))). This naming is also easy to remember: the a and d distributions in the middle indicate that car and cdr are called in turn.

We know that lists consist of ordered pairs.S expressions use parentheses to represent lists, so how can they represent more basic elements like ordered pairs? We can experiment:

`1`	`(cons 1 2) ;; '(1 . 2)`

If two elements in parentheses are separated by ., it means that it is an ordered pair. But if the second element of the ordered pair is enclosed in parentheses, the . and the parentheses of the second element are omitted:

1
2
3

'(1 . (2 . 3)) ;; '(1 2 . 3)
'((1 . 2) . (3 . 4)) ;; '((1 . 2) 3 . 4)
'(1 . (2 . (3 . (4 . ())))) ;; '(1 2 3 4)

Thus (cons 1 (cons 2 (cons 3 (cons 4 '()))))) results in '(1 2 3 4), which looks like a list now. The advantage of this syntax is that it reflects the fact that lists are made up of ordered pairs (which can be written explicitly as (+ . (2 . (3 . ())))), but also makes the list look comfortable (typically written (+ 2 3)).

5.3 Quasiquote and unquote

Scheme also provides a pair of special forms for constructing specific lists: quasiquote and unquote. They also take an S-expression as an argument. (quasiquote exp) can be abbreviated as `exp, and (unquote exp) can be abbreviated as ,exp. Like quote, quasiquote returns the S-expression as is, but evaluates the unquote part of it.

A similar syntax is unquote-splicing, which takes a list as an argument, (unquote-splicing list) is abbreviated as ,@list. It evaluates and expands the list:

(define items (list 10 20 30))

`(1 2 ,@items 3) ;; '(1 2 10 20 30 3)
`(,@(list 1 2) 3 4) ;; '(1 2 3 4)
`(,@'(1) 2 3) ;; '(1 2 3)

5.4 Common Functions

Here are some common functions for manipulating lists.

pair? Determines whether a list is an ordered pair.

(pair? 1) ;; #f
(pair? '()) ;; #f, NIL is not an ordered pair
(pair? (cons 1 2)) ;; #t
(pair? (list 1 2 3)) ;; #t, lists are also composed of ordered pairs

list? Determines if it is a list.

1
2
3

(list? '(1 2 3)) ;; #t
(list? '()) ;; #t, NIL is the empty list
(list? '(1 2 . 3)) ;;#f, does not end in NIL, not a list

symbol? Determines if it is a symbol.

(symbol? 12) ;; #f, numbers are not symbols
(symbol? 'abc) ;; #t
(symbol? (quote abc)) ;; #t
(symbol? pi) ;; #f, the value of pi is 3.14159, not a symbol
(symbol? 'pi) ;; #t
(symbol? '(1 2 3)) ;; #f, lists are not symbols

null? Determines if the list is empty.

(null? '()) ;; #t
(null? (list)) ;; #t
(null? (list 1 2)) ;; #f
(null? (cddr '(1 2))) ;; #t

memq Finds the ordered pair in the list where car is equal to the given value.

1
2
3

(memq 2 '(1 2 3)) ;; '(2 3)
(memq 3 '(1 2 3)) ;; '(3)
(memq 4 '(1 2 3)) ;; #f, returns false to indicate that it does not exist

assoc Assuming that the elements of the list are all ordered pairs, find the element of the ordered pair car that is equal to the given value.

1
2
3

(assoc 2 '((1 a) (2 b) (3 c))) ;; '(2 b)
(assoc 3 '((1 . a) (2 . b) (3 . c))) ;; '(3 . c)
(assoc 4 '((1 a) (2 b) (3 c))) ;; #f

append Connects two lists.

1
2

(append '(1 2 3) '(4 5)) ;; '(1 2 3 4 5)
(append '(1 2 3) '()) ;; '(1 2 3)

6 Functional Programming

Scheme advocates functional programming, and in addition to the fact that functions are first-class citizens, it also advocates “no assignment unless necessary”. So far, we haven’t introduced assignment statements. For imperative programming, you can’t even write a finite while loop without an assignment statement. In functional programming, however, we’re comfortable with all kinds of recursion.

(define (sum items)
  (if (null? items)
      0
      (+ (car items)
         (sum (cdr items)))))

(sum '(1 2 3 4)) ;; 10

Although it is not possible to change a variable by assignment, we can change the value of a parameter when we can call a function. One might argue that using recursion is poor performance because it consumes stack space. It’s true that the code above pushes the value of (car items) onto the stack before calling (sum (cdr items)), so that the sum can be calculated after sum returns. But we only need to change the way we write it a little:

(define (sum items)
  (define (iter i s)
    (if (null? i)
        s
        (iter (cdr i) (+ s (car i)))))
  (iter items 0))

We find that the return value of the recursive call (iter (cdr i) (+ s (car i))) is directly used as the return value of the original function (iter i s), and therefore does not need to be pushed onto the stack before being called. This is called tail recursion. Tail recursion is essentially iteration, because the recursive call to iter is a constant iterative update of the variables i and s.

6.1 Accumulate

We just defined a function that sums all the elements. What about the product of all the elements? We can define a product function.

(define (product items)
  (define (iter i p)
    (if (null? i)
        p
        (iter (cdr i) (* p (car i)))))
  (iter items 1))

We find that this function is almost identical to sum. Both functions, given an initial value, perform some operation with the elements of the list in turn, and then iterate through the list in turn; the only differences are in the initial value (0 in one case and 1 in the other) and the operation (+ in one case and * in the other). In Scheme, functions can be passed as values, and both + and * are functions. So we can define a generic function that passes initial values and operations as arguments:

(define (accumulate op init items)
  (define (iter i res)
    (if (null? i)
        res
        (iter (cdr i) (op res (car i)))))
  (iter items init))

(accumulate + 0 '(1 2 3 4)) ;; 10
(accumulate * 1 '(1 2 3 4)) ;; 24
(accumulate append '() '((1 2) (3 4 5) (a b c d))) ;; '(1 2 3 4 5 a b c d)

6.2 Map

A similar function is map. map maps each element of a list to a new value by a given function.

1
2

(map - '(1 2 3 4 5)) ;; '(-1 -2 -3 -4 -5)
(map (lambda (x) (* x x)) '(1 2 3 4 5)) ;; '(1 4 9 16 25)

map also supports passing multiple lists, as in (map proc list1 list2 ...) . These lists must be of equal length, and the number of lists must equal the number of arguments passed to the function. The elements of list1 are passed to proc as the first argument, the elements of list2 are passed to proc as the second element, and so on.

1
2

(map + '(1 2 3) '(10 20 30)) ;; '(11 22 33)
(map list '(1 2 3) '(a b c) '(x y z)) ;; '((1 a x) (2 b y) (3 c z))

How to implement map, Scheme supports defining functions with variable arguments. We can define (define (map proc . lists)), in which case lists is a list with the remaining arguments. Since (map proc list1 list2) can also be written as (map proc . (list1 list2)) (see Section 5.2), it is easy to see how this works.

Conversely, if there are n arguments stored in a list, they can be passed to a specified function with apply:

1
2

(apply + '(1 2)) ;; 3
(apply * '(2 3 4)) ;; 24

This allows us to implement the map function:

(define (map proc . lists)
  (if (null? (car lists))
      '()
      (cons (apply proc (map car lists))
            (apply map (cons proc (map cdr lists))))))

6.3 Filter

To filter out matching functions from a list, you can use filter. It accepts a function that returns a boolean value and a list as arguments, e.g.

1
2

(filter odd? '(1 2 3 4 5 6)) ;; '(1 3 5)
(filter even? '(1 2 3 4 5 6)) ;; '(2 4 6)

We can also implement filter:

(define (filter proc items)
  (cond [(null? items) '()]
        [(proc (car items))
         (cons (car items) (filter proc (cdr items)))]
        [else
         (filter proc (cdr items))]))

Can you change map and filter to iterative (tail recursive) form?

7 Assignment

Although functional programming discourages the use of assignments, there are many scenarios in which it would be inconvenient not to use assignments at all, and there are some scenarios in which appropriate use of assignments can improve code performance and simplify some implementations.Scheme performs assignments using the set! special form, which is used in the format (set! var val). set! evaluates a val expression and then assigns the value to var. Example:

(define a 1)
(set! a (+ a 1)) ;; a = 2
(set! a (* a 2)) ;; a = 4
(set! a (cons a (+ a 1))) ;; a = '(4 . 5)

Introducing assignment adds a lot of uncertainty to the system. For functions that do not use assignments, passing in a definite argument is bound to result in a definite value, just like a math function. Once assignment is introduced, this is not necessarily the case. You can see the following example:

(define (make-account n)
  (lambda (d)
    (set! n (+ n d))
    n))

(define account (make-account 0))

(account 10) ;; 10
(account 10) ;; 20
(account -5) ;; 15

Here (account 10) is called twice, passing in the same arguments but returning different values.Section 4.1 mentioned that when we pass a function as a value, the environment in which it resides is also passed. So we can use functions as data structures. The account above is a function that can also be thought of as a piece of data.

Once constructed, ordered pairs in Racket cannot be modified. We can implement a modifiable ordered pair using a function:

(define (mcons 1st 2nd)
  (let ([set-mcar! (lambda (v) (set! 1st v))]
        [set-mcdr! (lambda (v) (set! 2nd v))])
    (lambda (m)
      (cond [(eq? m 'mcar) 1st]
            [(eq? m 'mcdr) 2nd]
            [(eq? m 'set-mcar!) set-mcar!]
            [(eq? m 'set-mcdr!) set-mcdr!]))))

(define (mcar mpair) (mpair 'mcar))
(define (mcdr mpair) (mpair 'mcdr))
(define (set-mcar! mpair val) ((mpair 'set-mcar!) val))
(define (set-mcdr! mpair val) ((mpair 'set-mcdr!) val))

The above example can be thought of as “object-oriented programming” in Scheme. The functions returned by mcons are treated as objects, and the actions they perform are determined by the arguments passed to them, hence the message passing style. mcons can be called a constructor, and the return value of a constructor is called to get a “member”; an expression like (mpair 'mcar) is similar to mpair.mcar in Java. The following code shows some usage of mcons.

(define p (mcons 1 2))
(mcar p) ;; 1
(mcdr p) ;; 2
(set-mcar! p 10)
(set-mcdr! p 20)
(mcar p) ;; 10
(mcdr p) ;; 20

8 Summary

This article introduces some of the basics of Scheme, including the construction of S-expressions, the use of common special shapes, function calls and definitions, understanding the environment, ordered pairs and lists, the use of common functions, and assignment operations. These contents are enough to write many Scheme programs. In the next article, we will use Scheme to implement a Scheme interpreter, which implements most of the language features introduced in this article.

Table of Contents