Merkle trees are widely used in distributed systems. I first learned about this data structure when I was studying blockchain technology. But because it has hardly ever been used in my work, I have been plausible about the related concepts and features. Today, while studying the browser certificate transparency log, I read an article by Cloudflare, which also talked about the Merkle tree. The article is concise and clear, and immediately grasp the characteristics of the data structure and the problem to be solved.
The easiest way to understand data structures is to start from the problem, not from the definition. In the case of Merkle trees, it is to solve the problem of how to verify the data. Simply put, given a set of data, how to verify that some or all of it is accurate, or that none of it has been tampered with.
The most classic way to verify data integrity is to use a hashing algorithm.
For example, if the content of a file is “hello, world”, the corresponding MD5 hash value is as follows.
|
|
The key here is to calculate a hash value based on the file content. Whenever there is any change in the file content, then the calculated digest value will be different. This achieves the effect of data validation. Is there a case where the contents of two files are different, but the calculated hash value is the same? In reality, this situation can occur, but the probability of occurrence is very low and people usually assume that there will be no conflict. If it can occur, is it possible to artificially generate the file content so that its hash value is equal to some fixed value? Actually, it is possible. Again, because the probability is so low, it is often assumed to be ‘impossible’. That’s why hash functions are often also called one-way functions. That is, you can calculate the hash value from the content, and it is difficult to generate the content from the hash value in turn. But with the development of mathematical research and the increase in hardware speed, the probability of allowing a computer to generate the content with the specified hash value has increased greatly. One-way functions are also no longer one-way 😂 So the industry has begun to eliminate such as MD5/SHA1 this kind of weak strength hash algorithm, many times need to use SHA256 or even SHA512 and other high-strength algorithms. But no matter what, hash collisions are always a possibility.
The above is to do the checksum on a single file. Back to the beginning question, how to do checksum on multiple files? The most violent way is to concatenate the contents of all files and calculate the hash value together. It’s simple and brutal, and it really works. But isn’t it too wasteful to count all the files each time? If we have a clear suspicion that only a few of the files may be corrupted, is there any way to verify only a few of them?
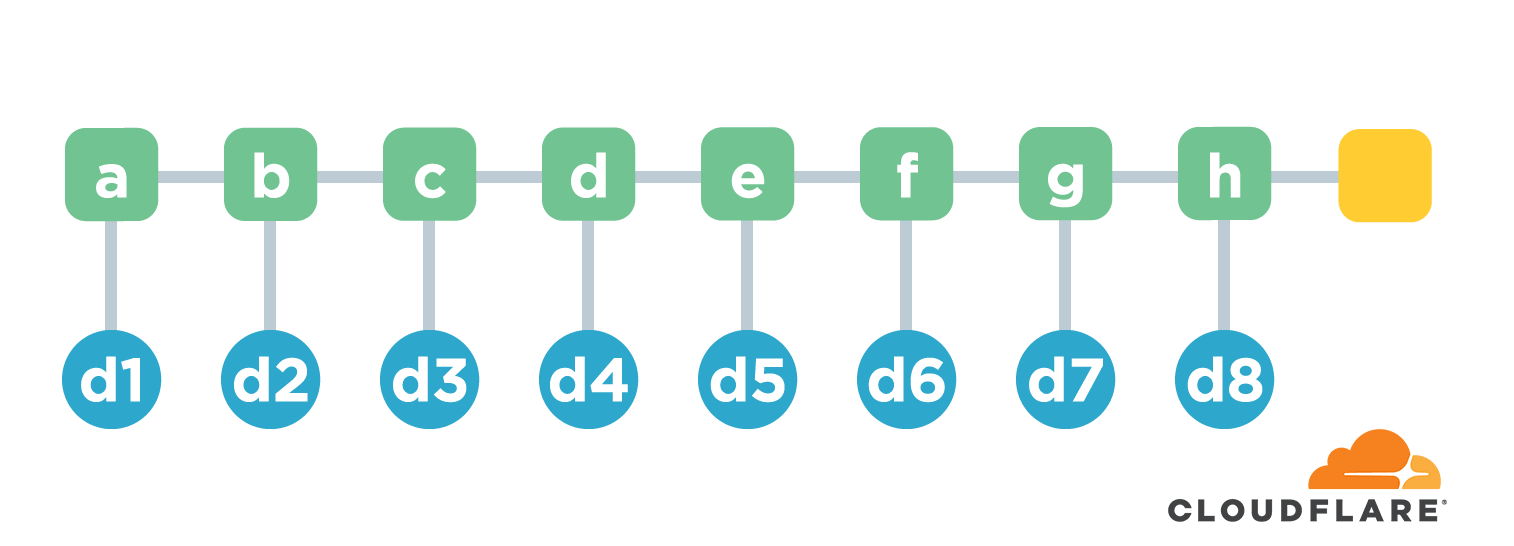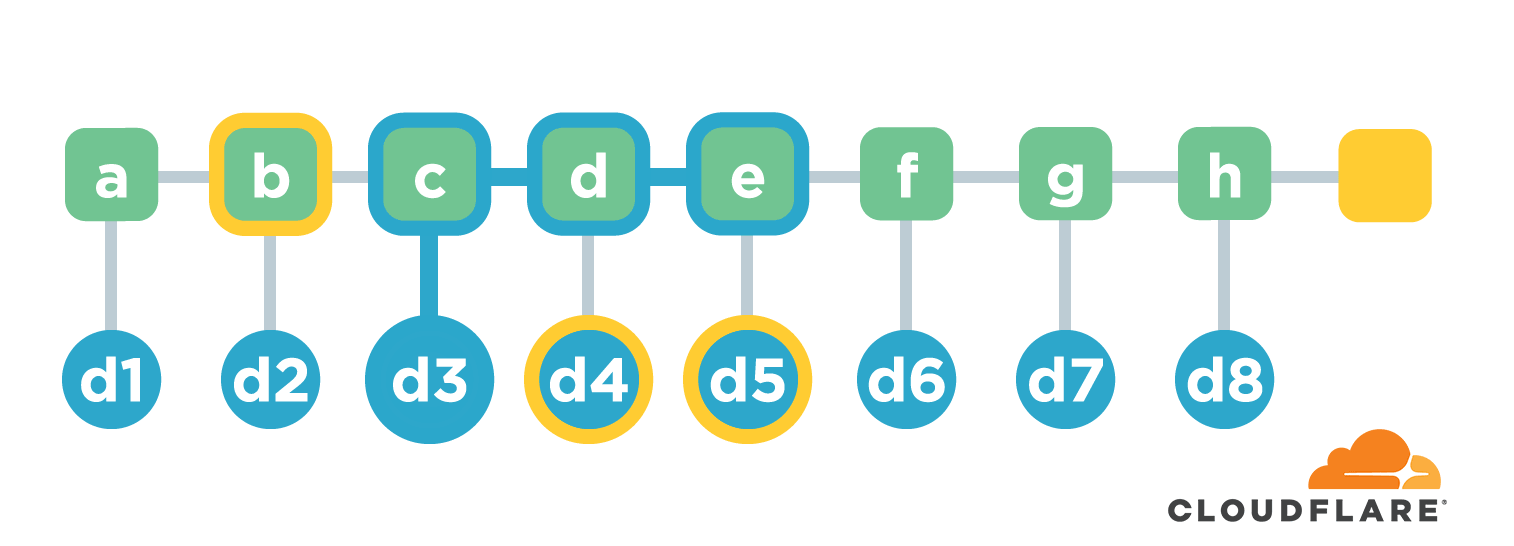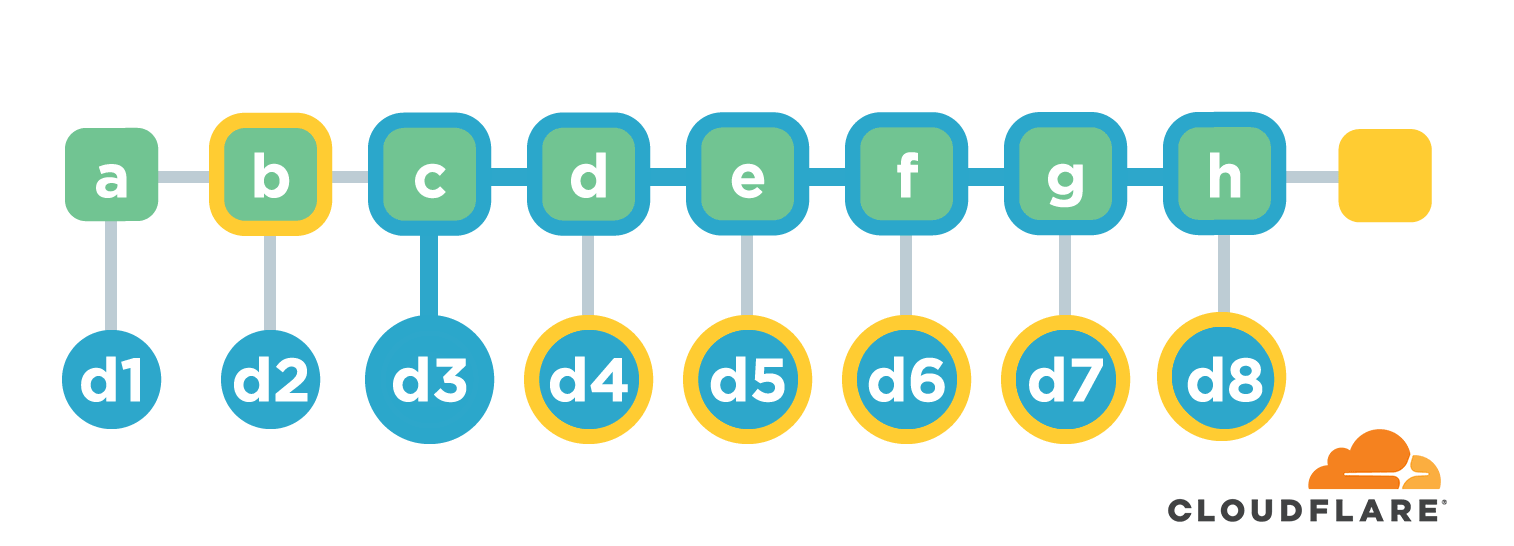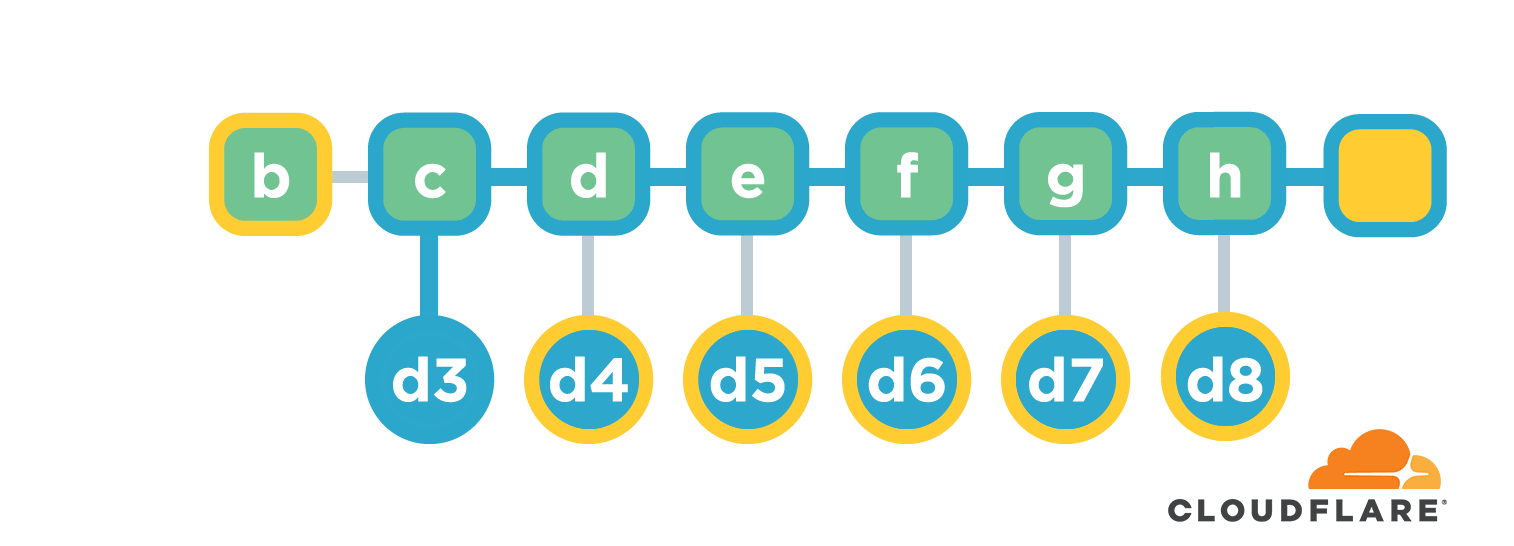
This requires the use of a chain structure. Chain structure is a name I invented myself 😄 It simply means that multiple files are arranged in some order. The hash value of the first file is calculated first. Starting from the second file, the calculation not only calculates the hash of the file itself, but also connects the hash of the file with the hash of the previous file and calculates another hash as the hash of that file.

Using the above figure as an example, we have a-h a total of 8 files. The hash value of the first file is d1=hash(a) . The hash from the second file is d2=hash(hash(b).d1) . Here the . means join two strings. And so on, we end up with a hash of d9=hash(h).d8 , which is used to represent the hash common to these 8 files. If the content of any file is corrupted or tampered with, the computed hash value will change. Well, the function is implemented.
The chain structure is efficient in generating hash values, and each time a new file is added, the new total hash value can be calculated based only on the original total hash value and the hash value of the new file. However, this structure is less efficient when verifying the content of the files. For example, if we want to verify the accuracy of d3, we need to know all the contents of files b-d and recalculate the hash value, and then compare it with the final hash value. This process can be very time consuming if there are many files.
Most of the general content checks are read more and write less. They are basically generated once, but may need to be repeatedly verified in different places. So we need a data structure that is easier and more efficient for the validation process. That’s what this article is about, the Merkle tree!
To transform an O(N) problem into an O(log2(N)) problem, you basically have to use a binary tree or dichotomy. A Merkle tree is a binary tree. After the files are ordered, the hash value of each file is first calculated, and this group is called the leaf node. Then every two hash values as a group, connected and then calculate the hash value. The result of the calculation is then grouped two by two, connected and calculated. And so on, until a unique hash value is calculated, which is used to represent the overall hash value of all files. The letters of the green nodes in the figure below indicate the hash values calculated at each level, and are for easy reference, not to be confused with the previous file names a-h. Only hash values are also kept in the Merkle tree.
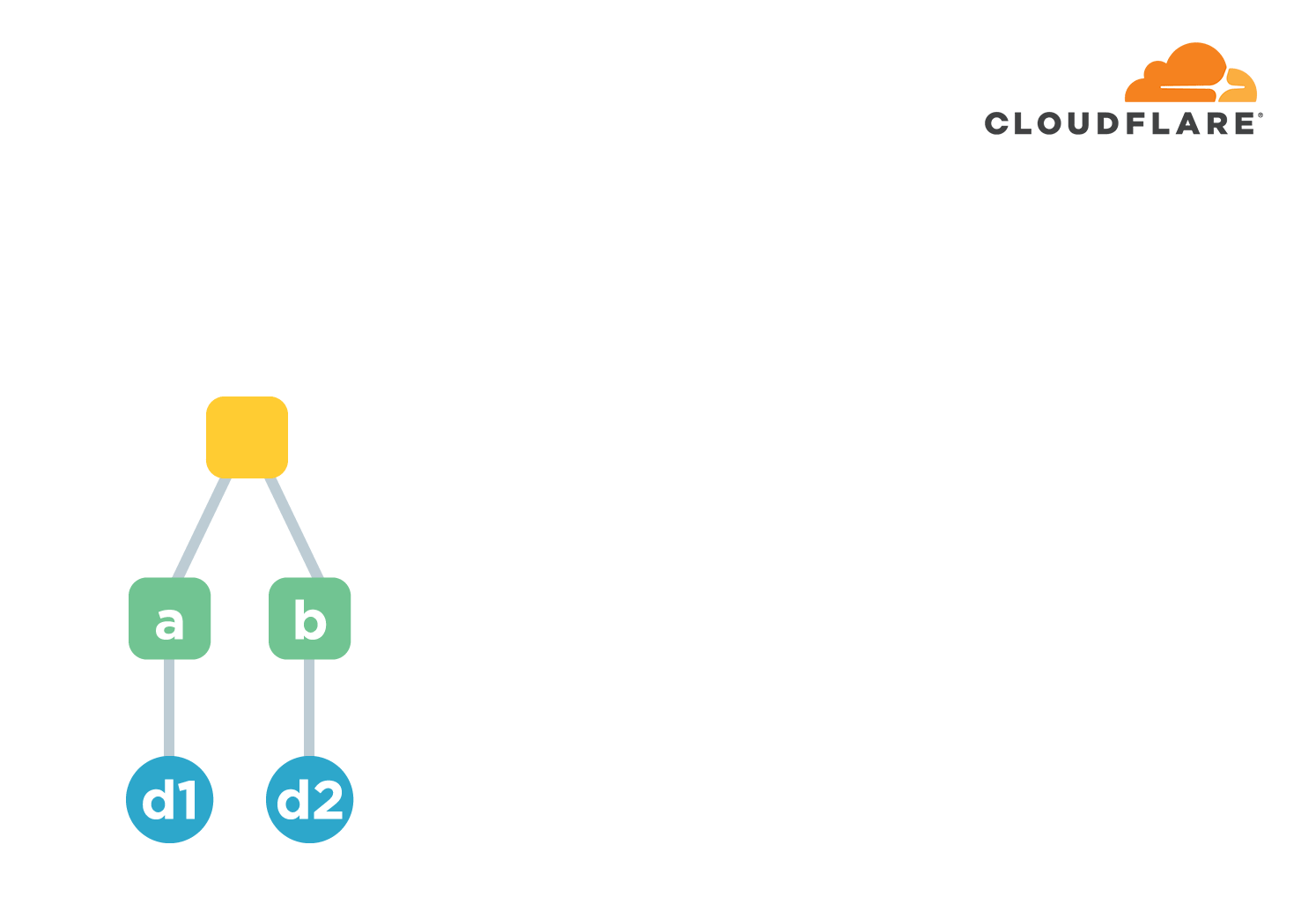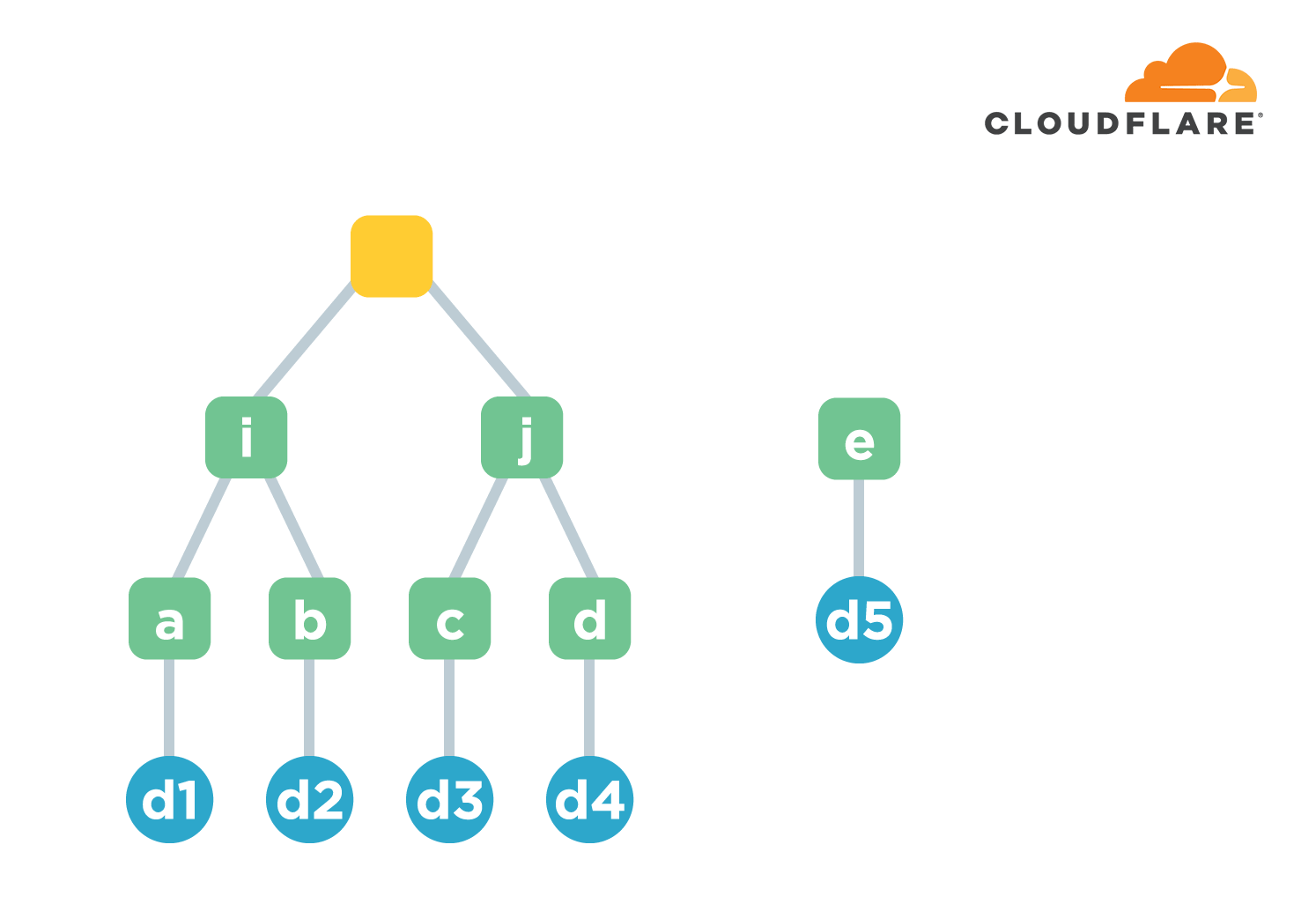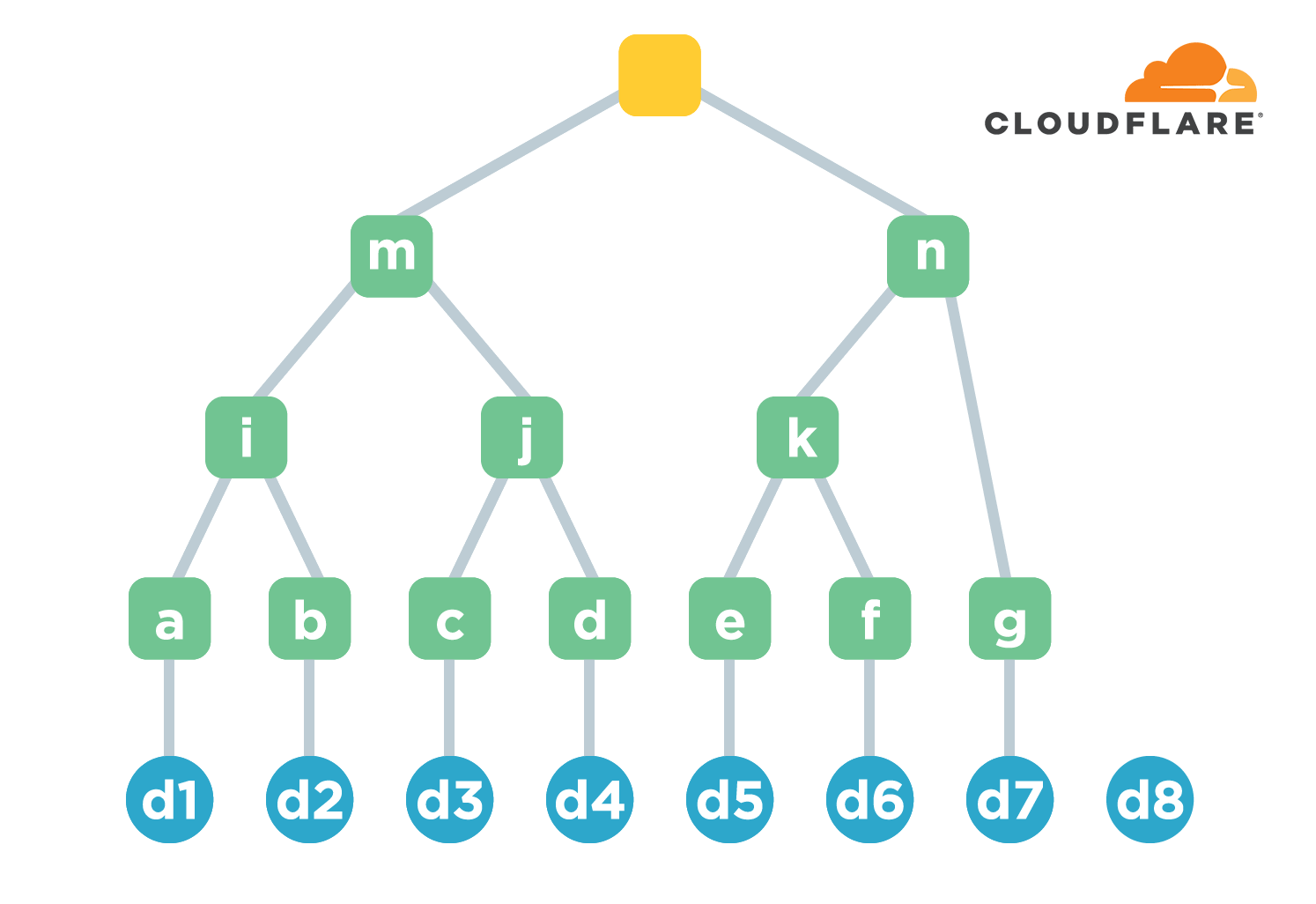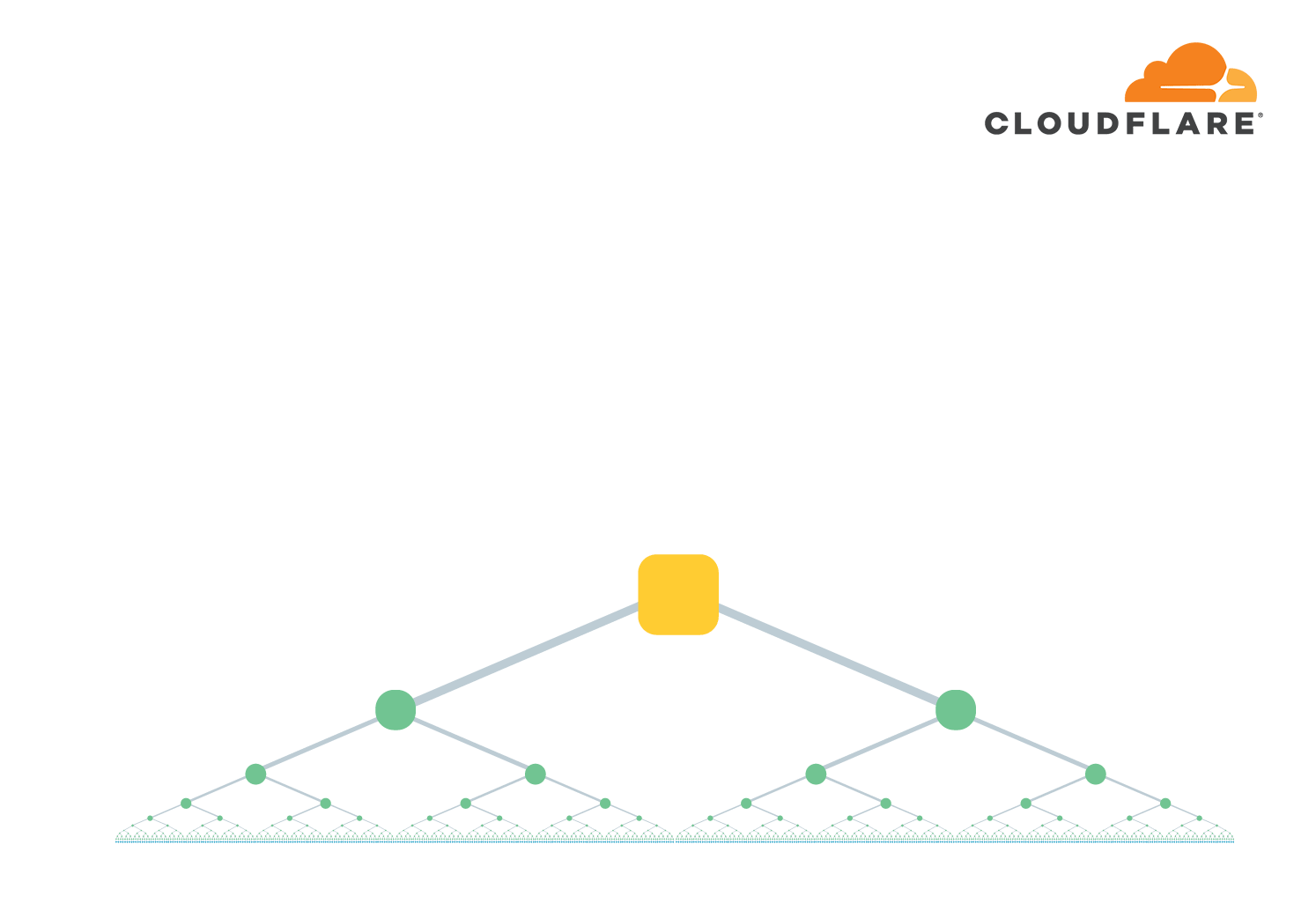
Obviously, if the number of files is N, then the height of the tree is basically log2(N). The maximum number of times the hash needs to be computed when adding a new file is the height of the tree, which is less efficient than the previous chain structure (because it is a constant). However, the check efficiency of Merkle tree is much improved.
Let’s take the example of verifying d3. First check the path from d3 to the root node, also called co-path, then find the direct children of each node on the path, i.e. i/d/n, and then calculate the root hash value. The computed hash is compared with the original one to determine whether d3 is valid, i.e. whether the contents of the corresponding file c are corrupted.
These are the main contents of the Merkle tree. When using it in practice, some details need to be handled. For example, in some implementations if the number of leaf nodes is not even, the last node will be made to repeat once, that is, to do a joint hash with itself. However, these treatments do not fundamentally affect the nature of the Merkle tree.
Merkle trees have many applications in distributed systems. None is more famous than Bitcoin’s blockchain. All transactions of Bitcoin are kept in different blocks in a decentralized manner. And in a particular block, the hashes of all the transaction data are organized into a Merkle tree, which is then saved to the block. The client can easily verify whether a particular transaction is valid or not! But probably the most widely used example is Git 😄 This is something you might not expect. In Git, each file generates a SHA1 hash based on its contents, and then a Merkle tree based on the directory structure, and the corresponding data is eventually saved to the commit record. But both blockchain and Git use a Merkle tree along with the chaining structure described earlier. Blocks are connected to each other and commits are connected to each other in a chained structure. That’s why once a transaction is saved to a block or a file is committed to Git, it’s very difficult to change it later. A local change will invalidate all the blocks or commits after it. You can do this in Git using things like rebase, but it’s almost impossible in a blockchain.
Because Merkle trees are a verifiable data structure, the industry also uses them to keep records of HTTPS certificate issuance. Every certificate issued by a CA vendor needs to write a log to a Merkle tree-based certificate transparency log system. Once submitted, it cannot be changed. The browser queries these logs when creating an encrypted connection to determine if a vendor has issued a certificate in error.