Radix Tree and Gin Implementation

Overview

Trie

Trie, also known as dictionary tree and prefix tree, is a multinomial tree structure, whose core idea is space for time, using the common prefix of strings to reduce unnecessary string comparisons to improve query efficiency. The figure below.

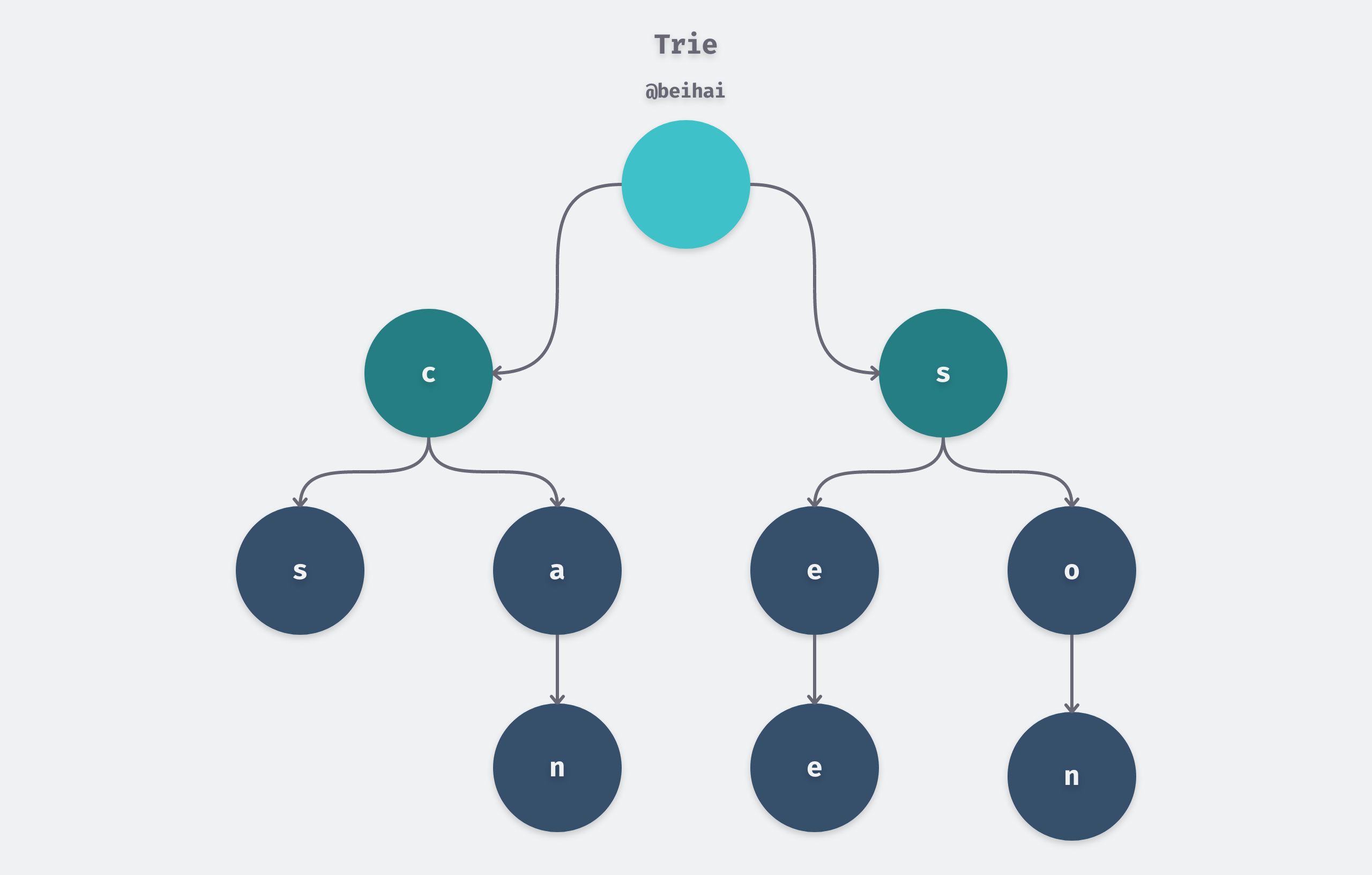
It can be seen that two keywords with a common prefix have the same path in the prefix part of Trie, so Trie trees are also called prefix trees.

The keyword word in Trie is usually a string, and Trie keeps each keyword in a path instead of a node. So usually the implementation sets a flag in the node to mark whether the keyword constitutes a keyword at that node. trie has the following properties.

1. for simplicity of implementation, the root node contains no characters and each child node other than the root node contains only one character.
2. the characters passed on the path from the root node to a node are concatenated as the string corresponding to that node.
3. all child nodes of each node contain different characters from each other.

The main problem is that the height of the tree depends on the length of the stored string, and the time complexity of querying and writing is O(m) , m being the length of the string, so the search time can be high.

Radix Tree

The Radix Tree, also known as the Compact Prefix Tree, is a spatially optimized Trie data structure. If a node in the tree is a unique child of a parent node, then that child node will be merged with the parent node, so a node in a Radix Tree can contain one or more elements. For example, if we have the keywords /App1/Config and /App/State, then their storage structure might look like the following.

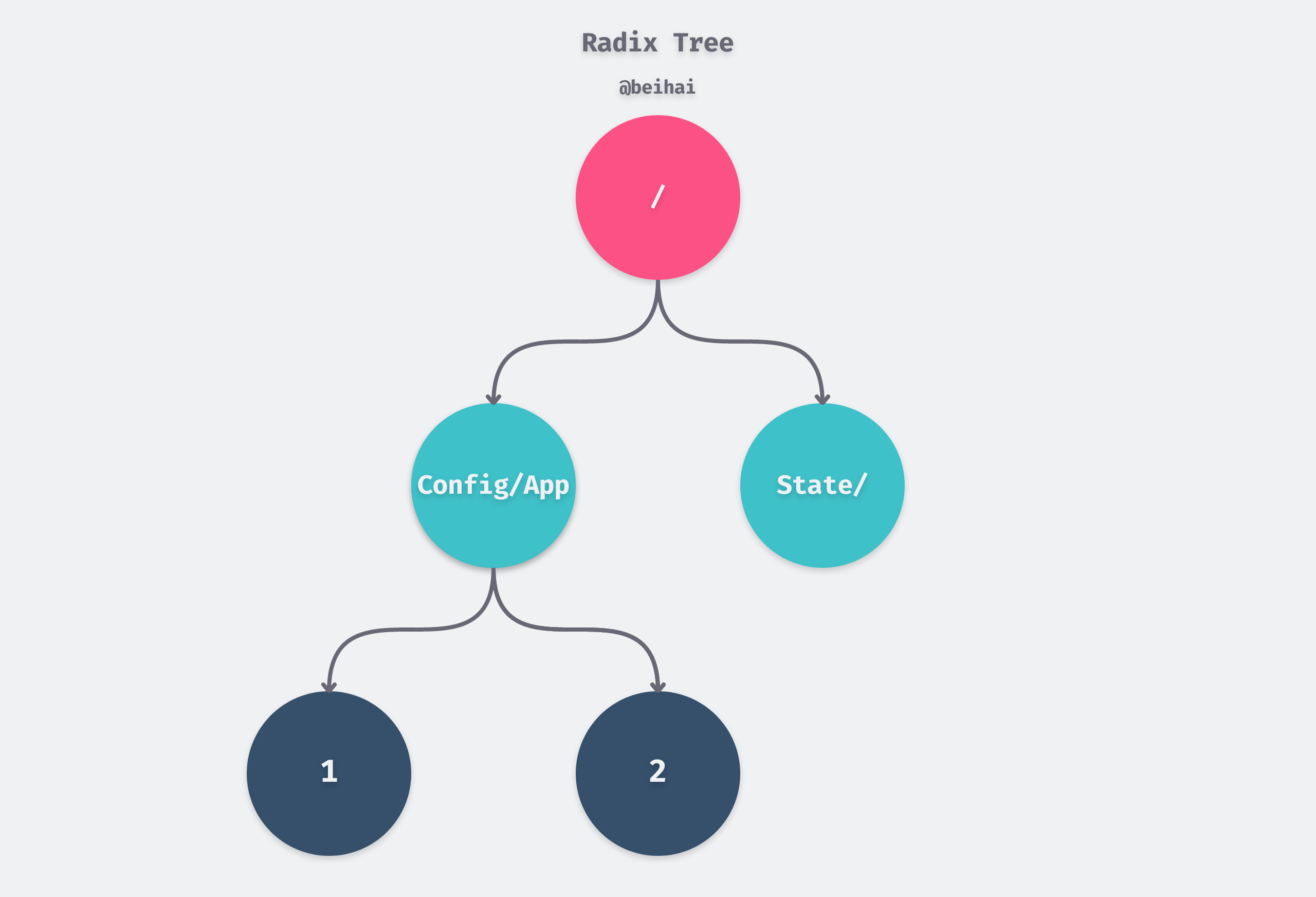
In general, Radix Tree, often used for IP routing, string matching and other scenarios with more of the same prefix and limited string length, is described below in the Gin Web framework for routing implementation.

Gin Routing Implementation

The Gin framework maintains a separate Radix Tree for each HTTP method, so the routing space for different methods is isolated.

1
2
3
4

type methodTree struct {
    method string
    root   *node
}

Each node of the Radix Tree stores not only the string of the current node, but also the full path of a route. In addition to this, the query process has been optimized, with the indices field holding the first character of the child node to quickly determine which child node the current path is in.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

type node struct {
    path      string        // This node corresponds to the path
    indices   string        // The set of the first characters of the child path
    wildChild bool          // Whether the child node contains a wildcard node
    nType     nodeType      // Current Node Type
    priority  uint32        // Priority, number of handlers registered for child nodes, subchild nodes, etc.
    children  []*node       // The set of child nodes, each child can contain only one parameter node, and the last position in the set
    handlers  HandlersChain // Processing function chain
    fullPath  string        // Full path
}

Routing Registration

The logic of Radix Tree writing data is not complicated, if the length of the common prefix is less than the length of the string saved in the current node, then it will split the current node, otherwise it recursively enters the child nodes for operation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

// The code has been trimmed
func (n *node) addRoute(path string, handlers HandlersChain) {
    fullPath := path
    n.priority++

    // Direct insertion of empty nodes
    if len(n.path) == 0 && len(n.children) == 0 {
        n.insertChild(path, fullPath, handlers)
        n.nType = root
        return
    }

    parentFullPathIndex := 0

walk:
    for {
        // Find the longest common prefix
        i := longestCommonPrefix(path, n.path)

        if i < len(n.path) {
            // If the length of the common prefix is less than the length of the string saved by the current node, split the current node
        }

        // Insert child node
        if i < len(path) {
            path = path[i:]
            c := path[0]
        
            n.insertChild(path, fullPath, handlers)
            return
        }

        return
    }
}

Route matching

Gin queries the route via the node.getValue() method, and the core logic in this extra-long function is the following breadth-first traversal.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

walk: // Outer loop for walking the tree
    for {
        prefix := n.path
        if len(path) > len(prefix) {
            if path[:len(prefix)] == prefix {
                path = path[len(prefix):]

                // Try all the non-wildcard children first by matching the indices
                idxc := path[0]
                for i, c := range []byte(n.indices) {
                    if c == idxc {
                        n = n.children[i]
                        continue walk
                    }
                }
        }
    }
    }