B-Tree and its variants data structures are widely used in storage systems, database systems, mainly as indexes for dynamic random access data scenarios. google/btree (github.com) is a pure in-memory B-Tree implementation written in Go, and its source code is analyzed in this paper.

Overview

B-Tree structure

Organization and maintenance of large ordered indices This paper presents the B-Tree data structure. The query of B-Tree starts from the root node and performs a dichotomous lookup of the ordered data within the node and ends the query if it hits, otherwise it goes to the child node query up to the leaf node.

The characteristic of B-Tree query is that the search may end at a non-leaf node. As a typical tree structure, it contains the following node types.

  • Root Node: A B-Tree has only one root node, which is located at the top of the tree.
  • Branch Node: contains data items and pointers to child nodes.
  • Leaf Node: stores only data items.

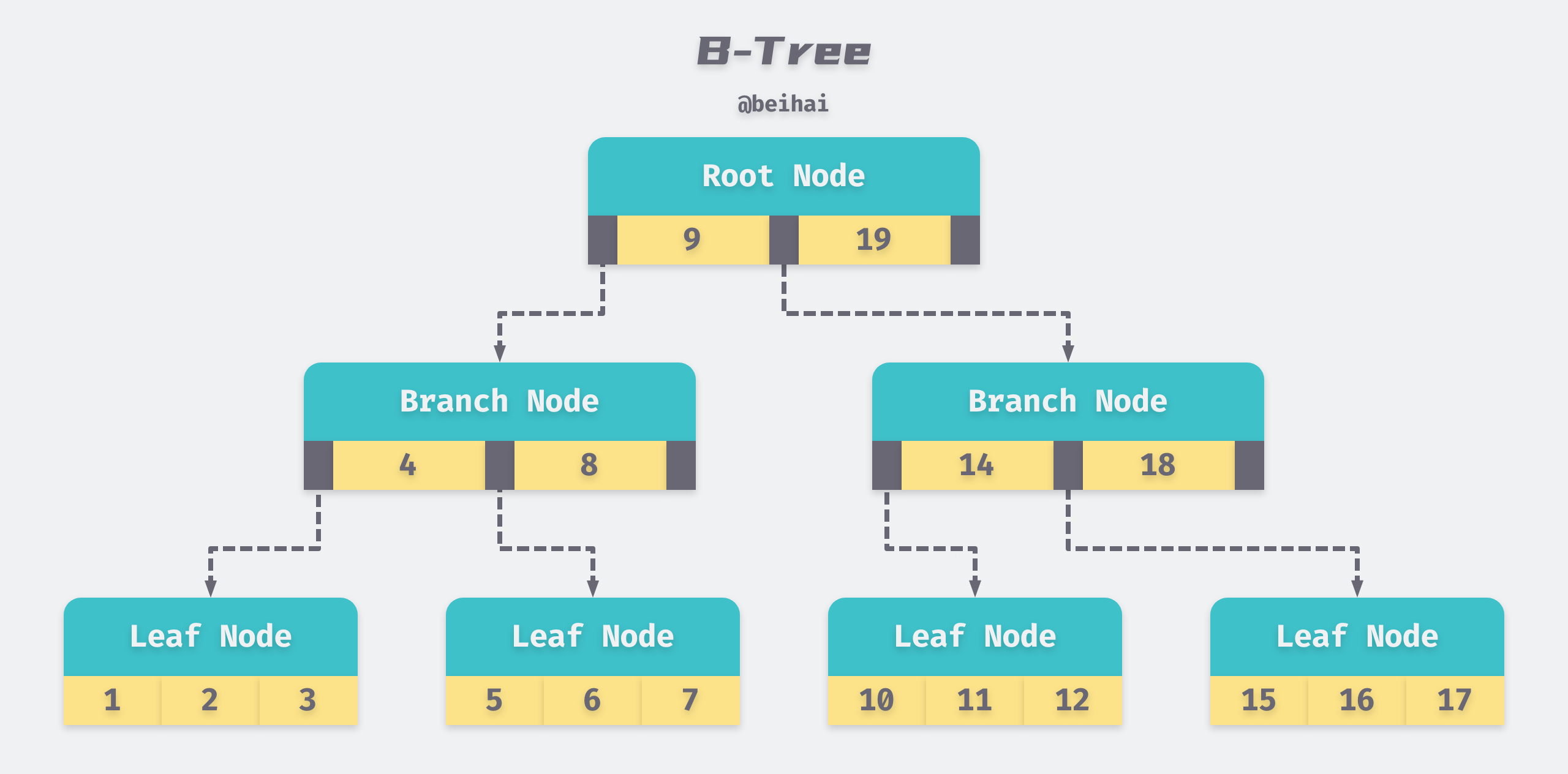
B-Tree

The structure of a B-Tree is shown in the figure above. A non-empty B-Tree with height h and minimum degree k has the following properties.

  1. the length from the root to the leaf nodes is h.
  2. root and leaf nodes can contain [1, 2k] data, and the number of children of root and branch nodes is the number of data in that node + 1.
  3. all nodes except root and leaf nodes have at least k data and at most 2k data.
  4. all nodes except root and leaf nodes have at least k+1 child nodes and at most 2k+1 child nodes.

API

btree provides the basic CRUD APIs. The comments describe the functionality of these interfaces in detail, and you can Google many articles about the use of btree. Therefore, only a few key APIs are listed to facilitate understanding of the following.

1
2
3
4
5
6

func (t *BTree) Get(key Item) Item {}
func (t *BTree) ReplaceOrInsert(item Item) Item {}
func (t *BTree) Delete(item Item) Item {}
func (t *BTree) Has(key Item) bool {}
func (t *BTree) Clear(addNodesToFreelist bool) {}
func (t *BTree) Clone() (t2 *BTree) {}

The Item interface needs to be implemented before data can be inserted into the btree, and this interface contains only one Less method, which is used to sort all the data in the btree in increasing order.

1
2
3

type Item interface {
  Less(than Item) bool
}

Passing values through the interface is a layer of abstraction for data compatibility across data types, rather than serializing data into byte slice for storage. The disadvantage is that type assertions and conversions are required each time the value is read, but usually the API is wrapped in a layer so that the caller does not have to pay attention to this content.

Strict Weak Ordering

An important concept in btree is Strict Weak Ordering: i.e. if ! (a<b) && ! (b<a), then a and b are considered to be equal. Here, equivalence does not mean that a and b are the same object entity or that their values are identical, but rather that a and b are equal if they satisfy the expression ! (a<b) && ! (b<a) can be considered as a == b.

For example, in the following code example, the foo structure has three internal fields and implements the Less method, which can be considered a less-than < operator. a and b are both its two entity objects, and the structure does not manually implement the == operator. Although they have different variable values and memory addresses, they satisfy the condition ! (a<b) && ! (b<a), then a and b can be considered equal.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

type foo struct {
  key   int64
  value int64
  name  string
}

func (i *foo) Less(b *foo) bool {
  return i.key < b.key
}

func main() {
  a := &foo{key: 123, value: 456, name: "test1"}
  b := &foo{key: 123, value: 789, name: "test2"}
  if !a.Less(b) && !b.Less(a) {
    println("a == b")
  }
}

Specifically in the query method implementation of the btree, a dichotomous lookup is used to find the first value that satisfies the (item < s[i]) condition. This means that (item < s[i-1]) is not valid (the value is false), and then (s[i-1] < item) is judged again, and if it is not valid either, then item is considered equal to s[i-1].

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 'found' is true if the item already exists in the list at the given index.
func (s items) find(item Item) (index int, found bool) {
  i := sort.Search(len(s), func(i int) bool {
    return item.Less(s[i])
  })
  if i > 0 && !s[i-1].Less(item) {
    return i - 1, true
  }
  return i, false
}

Data structure

The data structure of btree is relatively clear, containing the minimum degree degree of the B-Tree, the number of data entries stored length, and the root node root. Each node contains its own child nodes and data entries.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// Write operations are not safe for concurrent mutation by multiple goroutines, but Read operations are.
type BTree struct {
  degree int
  length int
  root   *node
  cow    *copyOnWriteContext
}

type node struct {
  items    items
  children children
  cow      *copyOnWriteContext
}

type children []*node

btree does not distinguish between different types of nodes, they are uniformly represented as node to reuse the code for node operations. If the node is a leaf node, then its children field is empty.

copyOnWriteContext

copyOnWriteContext is a structure held by every node in the btree, and as you can see from the name, it is a copy-on-write related content. Since btree is a pure memory implementation, when we copy the original btree using the Clone() method provided internally, the new tree and the old tree will share the same memory space using the copy-on-write technique, thus saving memory overhead and the time needed to copy the data. Only when a node is to be written to is a new node actually created.

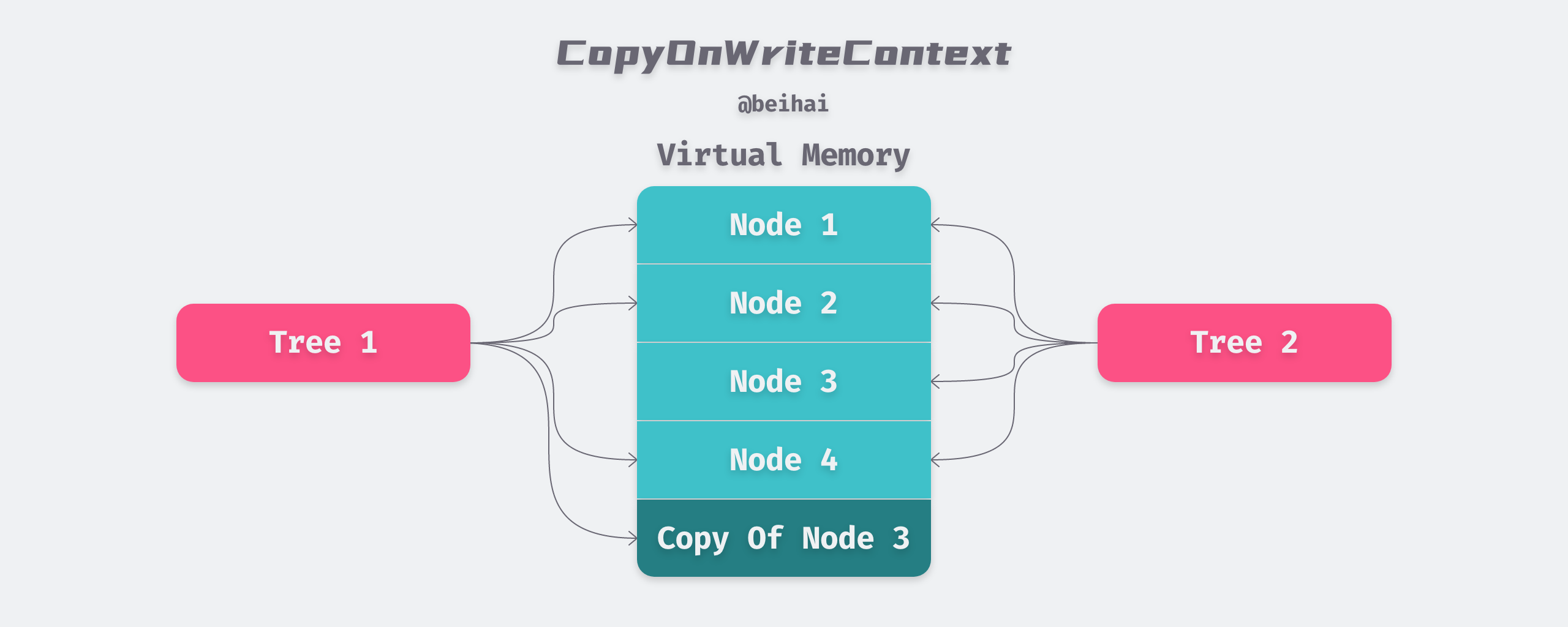
copyOnWriteContext

1
2
3
4
5
6
7
8

type copyOnWriteContext struct {
  freelist *FreeList
}

type FreeList struct {
   mu       sync.Mutex
   freelist []*node
}

The Redis RDB persistence also uses COW technology, where the Redis master process forks out the child processes for data backup, and the parent process continues to provide services to the outside world. The child and parent processes only have different virtual spaces, but the corresponding physical spaces are the same, which is similar to the Clone() method. The difference is that btree’s copy-on-write directly shares the virtual memory address.

Taken as a whole, copyOnWriteContext has two roles.

  • Mark whether btree has write access to the current node, if not, a new node needs to be created and replace the current node before a write operation can be performed.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

    func (n *node) mutableFor(cow *copyOnWriteContext) *node {
if n.cow == cow {
    return n
}
out := cow.newNode()
// copy node to out code is omitted
return out
}

func (c *copyOnWriteContext) newNode() (n *node) {
n = c.freelist.newNode()
n.cow = c
return
}

    The mutableFor method of the node demonstrates this process. If the cow of the current node is the same as the cow of the btree, then the current node is returned directly, otherwise a new node is created and the value of the current node is copied to the new node.

  • Encapsulates the reusable node node list freelist, which is put into the recycle list when a node is destroyed, and can be directly retrieved for reuse when a new node is created, reducing the frequency of node memory requests.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

    func (f *FreeList) newNode() (n *node) {
f.mu.Lock()
index := len(f.freelist) - 1
if index < 0 {
    f.mu.Unlock()
    return new(node)
}
n = f.freelist[index]
f.freelist[index] = nil
f.freelist = f.freelist[:index]
f.mu.Unlock()
return
}

copyOnWriteContext is an important means for btree to optimize memory overhead, reducing the frequency of memory requests and destruction from both reuse/shared memory perspectives, and using copy-on-write to share the same data in high-volume data replication scenarios.

External Interfaces and Applications

ReplaceOrInsert

ReplaceOrInsert inserts a new piece of data into the btree, replacing the old value with the new one if it already exists. The implementation of this interface removes the boundary condition handling and essentially calls the internal insert method to insert the data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

func (t *BTree) ReplaceOrInsert(item Item) Item {
  // ...
  out := t.root.insert(item, t.maxItems())
  if out == nil {
    t.length++
  }
  return out
}

func (n *node) insert(item Item, maxItems int) Item {
  i, found := n.items.find(item)
  if found {  // The data exists in the current node, update the data
    out := n.items[i]
    n.items[i] = item
    return out
  }
  if len(n.children) == 0 {  // The current node has no children, insert new data in the current node
    n.items.insertAt(i, item)
    return nil
  }
  if n.maybeSplitChild(i, maxItems) {
    inTree := n.items[i]
    switch {
    case item.Less(inTree):
      // no change, we want first split node
    case inTree.Less(item):
      i++ // we want second split node
    default:
      out := n.items[i]
      n.items[i] = item
      return out
    }
  }
  return n.mutableChild(i).insert(item, maxItems) // Recursive calls
}

The execution path of the insert method is as follows.

  1. first determine whether the data exists in the current node, and if so, update the data.
  2. if the data does not exist in the current node and the current node has no children, then insert the new data directly in the current node.
  3. if the data does not exist in the current node, and the current node contains children, then recursively call the insert method of the children. As mentioned in the Strict Weak Ordering subsection, the find method returns i as the first value that satisfies the (item < s[i]) condition. Since it has been determined that the data does not exist in the current node, it should be stored in the i-th child node.

Delete

The following judgments are required when deleting data from a B-Tree node.

  • If the number of items in the node is greater than minItems, the specified item is deleted directly from the node.
  • If the number of items in the node is less than or equal to minItems, then you need to fill the node with items:
    1. the left node contains enough items, steal an item from the left node.
    2. the right node contains enough items, steal an item from the right node.
    3. merge with the right node.

The btree simplifies the delete operation somewhat by ensuring that the child node has enough items to remove the node before recursively calling the remove method on the child node, and then calling the remove method again to actually remove the data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

// The following code has been simplified
func (n *node) remove(item Item, minItems int, typ toRemove) Item {
  i, found := n.items.find(item)
  if len(n.children) == 0 {
    if found {
      return n.items.removeAt(i)
    }
    return nil
  }
  // If we get to here, we have children.
  if len(n.children[i].items) <= minItems { // Child nodes need to be populated with item
    return n.growChildAndRemove(i, item, minItems, typ)
  }
  child := n.mutableChild(i)
  if found {
    out := n.items[i]
    n.items[i] = child.remove(nil, minItems, removeMax)
    return out
  }
  return child.remove(item, minItems, typ)
}

// growChildAndRemove Make sure the child node contains enough items
func (n *node) growChildAndRemove(i int, item Item, minItems int, typ toRemove) Item {
  if i > 0 && len(n.children[i-1].items) > minItems {
    // Steal from left child
  } else if i < len(n.items) && len(n.children[i+1].items) > minItems {
    // steal from right child
  } else {
    // merge with right child
  }
  return n.remove(item, minItems, typ) // The second call to the remove method actually removes the item
}

Iterate

The btree supports incremental/descending range queries, in the case of incremental queries, this is a standard iterative BFS implementation and iterates over the values with the ItemIterator function passed in by the caller.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

func (n *node) iterate(dir direction, start, stop Item, includeStart bool, hit bool, iter ItemIterator) (bool, bool) {
  var ok, found bool
  var index int
  switch dir {
  case ascend:
    if start != nil {
      index, _ = n.items.find(start)
    }
    for i := index; i < len(n.items); i++ {
      if len(n.children) > 0 {
        if hit, ok = n.children[i].iterate(dir, start, stop, includeStart, hit, iter); !ok {
          return hit, false
        }
      }
      // Removed boundary condition handling code
      if !iter(n.items[i]) {
        return hit, false
      }
    }
    if len(n.children) > 0 {
      if hit, ok = n.children[len(n.children)-1].iterate(dir, start, stop, includeStart, hit, iter); !ok {
        return hit, false
      }
    }
  return hit, true
}

Application

etcd saves each version of the key-value pair reversion to BoltDB in order to achieve multi-version concurrency control. In order to associate the original key-value pair information provided by the client with the reversion, etcd uses btree to maintain the mapping between Key and reversion, and then uses the obtained reversion to find the value in BoltDB.

The following is etcd’s wrapped btree code. Since btree supports concurrent reads, but only serial writes, a read/write lock is added to treeIndex, which is not described in detail in this article.

1
2
3
4
5

type treeIndex struct {
  sync.RWMutex
  tree *btree.BTree
  lg   *zap.Logger
}

Summary

The Google implementation of btree has many points to consider, using write-time copy and recycle lists to reduce memory overhead and reuse the underlying code as much as possible, and the overall design is very clean.

From the above, we know that the performance of B-Tree lookup is unstable, with the best case being only the root node and the worst case being the leaf node. And as an ordered combination of data, its range query performance is not good either. Therefore, an improved data structure B+Tree is proposed based on the B-Tree.

  • All nodes of B-Tree store data, while only leaf nodes of B+Tree store data with stable query complexity of log(n),.
  • The leaf nodes of B+Tree add pointers to the left and right nodes, i.e., it becomes a chain table structure, and degenerates from BFS to chain table traversal when performing range queries.

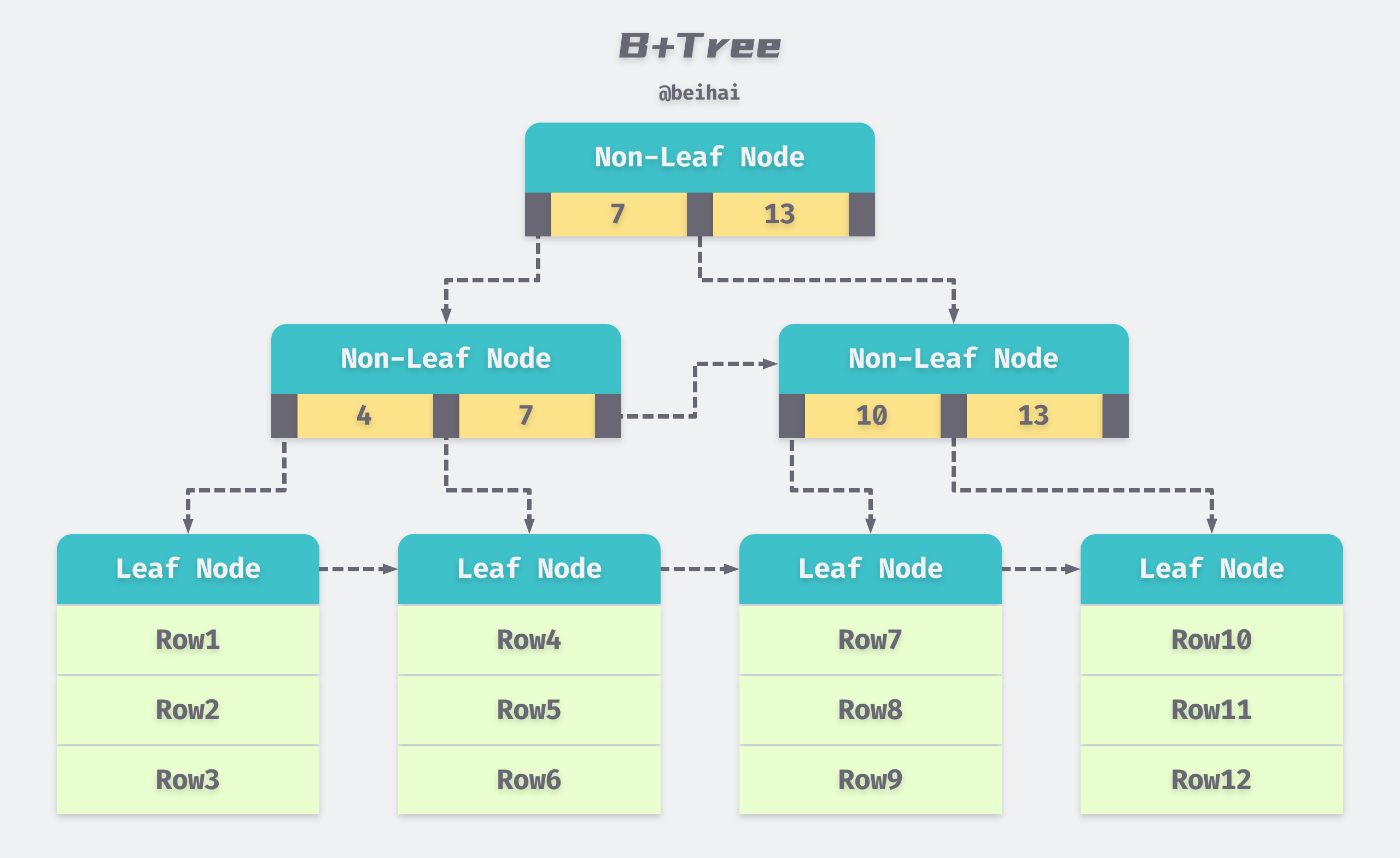
B+Tree

Another advantage of the B+Tree is that a non-leaf node of the same size can be indexed to more child nodes because the non-leaf nodes do not store data, only the key and a pointer to the child nodes. For example, if we implement a disk-based indexing system with a fixed size of 16KB per node and 1KB per piece of data, with a unit64 integer as the primary key and a unit64 pointer to a child node, that is, a node can store 16 pieces of data. Then the B+Tree with height 3 has 1 root node in the first layer, 1,000 nodes in the second layer (16 Bytes for a primary key and a pointer), and 1,000,000 nodes in the third layer, which can store about 16 million pieces of data. The B-Tree has only 16 nodes in the second layer and 256 nodes in the third layer, which can only store 4096 data, so it takes 6 layers to store 16 million data.

From the above example, we can see that in the case of tens of millions of data, without considering caching nodes in memory, B-Tree requires at worst 6 I/Os to query the data, while B+Tree is stable at 3 I/Os.

Therefore, in my opinion, B-Tree has no advantage in disk-based storage systems for either single-value queries or range queries, and in pure in-memory storage, B-Tree is only suitable for infrequent range queries.

References