One of the most important abstractions in distributed systems is consensus: all the nodes agree on a certain proposal. One or more nodes in a distributed system can propose certain values, and a consensus algorithm will decide the final value, while the core idea of consensus is that the decision is unanimous and once decided, it cannot be changed. This article summarizes some common consensus algorithms and theories in the distributed domain, hoping to gain a more comprehensive knowledge.

Consensus and Consistency

Unreliable networks and clocks

The Internet and the internal networks of most data centers are asynchronous networks in which a node can send a packet to another node, but the network does not guarantee when it will arrive, or even if it will arrive at all. While waiting for a response after sending a message, many error conditions may occur.

  • the request may be in a message queue somewhere or a network partition may occur and not be immediately communicated to the remote receiving node.
  • The remote receiving node may have crashed and failed or be temporarily unable to respond (e.g. running a long garbage collection).
  • The remote receiving node may have processed the request correctly, but the reply message is lost in the network.

When sending packets over the network, packets can be lost or delayed, and similarly, this can happen with reply messages. These problems cannot be clearly distinguished in an asynchronous network; the only thing the sender can be sure of is that a response message has not yet been received, but there is no way to tell exactly why; typically, the message sender keeps sending the message repeatedly in anticipation of a response.

A common error situation in distributed systems is that since cross-node communication cannot be completed immediately, messages always take time to travel from one machine to another via the network, but due to the uncertain latency of the network, we cannot provide a guarantee that messages are received in the order in which they were sent, i.e., messages sent later may arrive for processing first, or messages are repeatedly processed, which violates the consistency requirements.

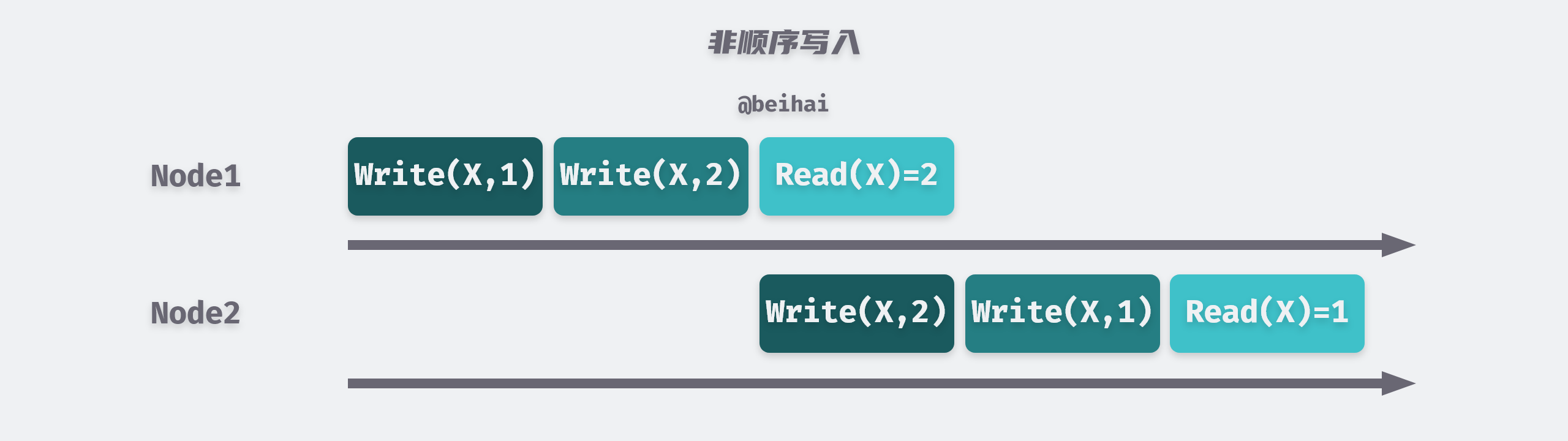
Non-sequential writing

So the asynchronous network of distributed systems is unreliable; it cannot guarantee the order of messages. One strategy to solve the above data conflict problem is Last Write Wins (LWW) : When writes are copied to other nodes, the events are marked in order according to the wall clock of the source write node, and the most recent write data in time is adopted.

Modern computers have at least two different clocks internally; the wall clock returns the number of seconds or milliseconds since January 1, 1970, the UNIX timestamp; the monotonic clock is a monotonically self-increasing time counter commonly used to measure sustained intervals of time.

Each computer has its own quartz clock device, which means that each machine maintains its own local version of time. But these quartz clock devices are not absolutely accurate and may suffer from clock drift (running faster or slower), and the time on one node may be completely different from the time on another node. For example, Google assumes that its servers have a clock drift of 200 ppm (parts per million), which corresponds to a maximum possible deviation of 6ms if it resynchronizes with the NTP server every 30 seconds, or 17s if it synchronizes once a day.

Since the last message written is determined by the clock on a node, this does not avoid the fact that this clock could be wrong. So sorting events across nodes by timestamps still does not solve the following types of problems.

  • write operations that occur later may not overwrite the value of the earlier version, because the clock of the latter node is too fast, causing some data to be secretly discarded.
  • two nodes may produce exactly the same timestamp due to clock precision limitations.
  • leap seconds can produce an adjustment of one minute to 59 or 61 seconds, which may confuse the system.

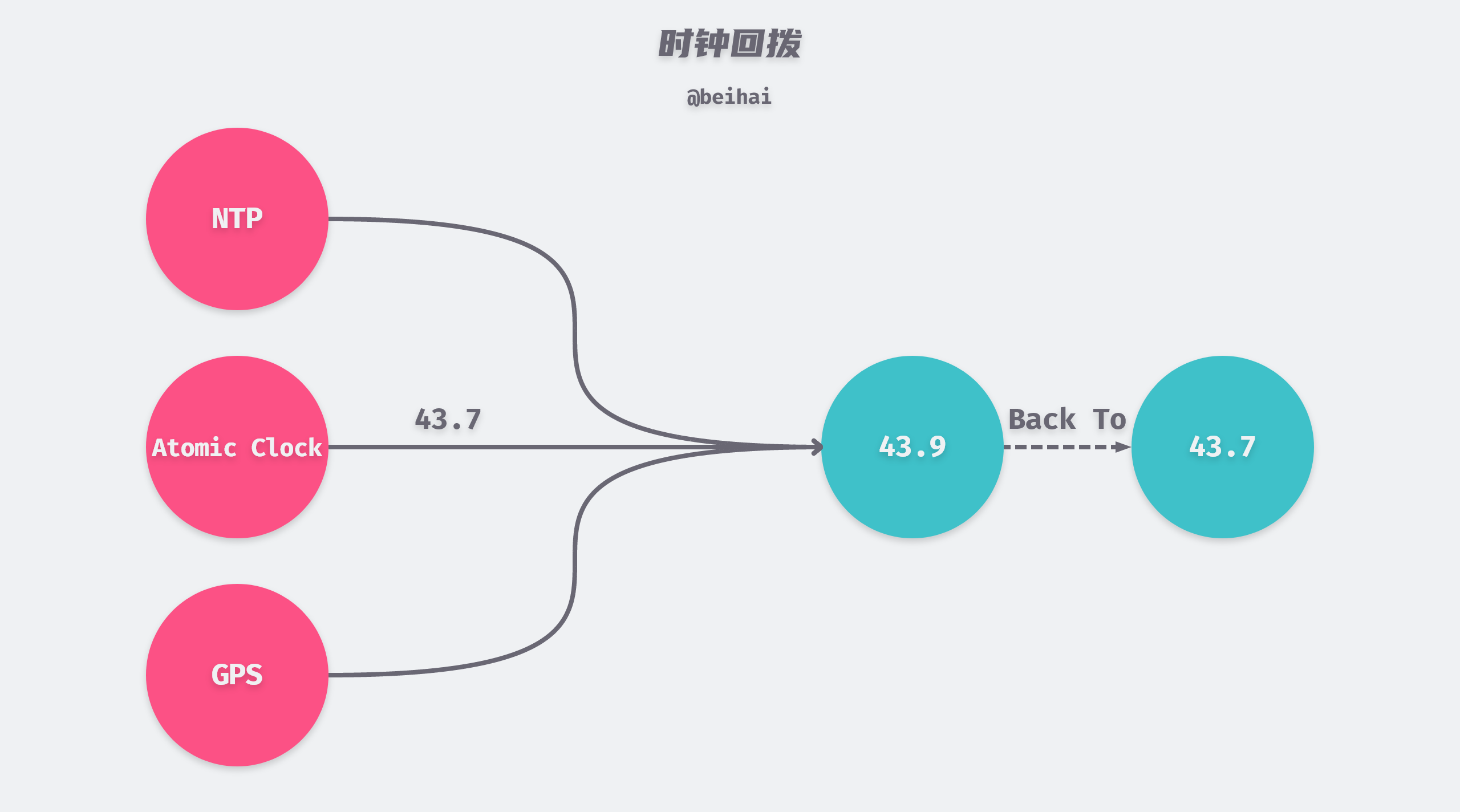
While wall clocks can be synchronized with more accurate clocks such as NTP (Network Time Protocol) servers, GPS, or atomic clocks set up inside the data center to correct their own time, if the clocks are far apart, applications may see sudden backward or forward jumps in time after a time reset, which can cause a new clocking problem: NTP synchronization may create a clock rollback, making the later-written data have an older=earlier timestamp, causing that write to be discarded.

Clock callback

FLP Impossibility Theorem

The FLP Impossibility Theorem is one of the most important theorems in the history of distributed systems, and the FLP paper Impossibility of Distributed Consensus with One Faulty Process proves the conclusion that in an asynchronous system model, there does not exist a deterministic algorithm that can always reach consensus in finite time if there is a risk of node collapse failure. The impossibility theorem is a proof based on the asynchronous system model, which is a very restricted model that assumes that the consensus algorithm cannot use any clock or timeout mechanism to detect crashed nodes and that messages will be transmitted only once.

However, in practice, each node has its own wall clock and monotonic clock, and although they may have completely different times, the frequency of time updates is exactly the same, so we can still calculate the interval between received messages by clocks, and under this premise, it is possible to use methods such as timeouts to determine whether a node survives, thus bypassing the FLP theorem to achieve a stable consensus scheme.

In summary, the FLP theorem actually tells us not to waste time trying to design consensus algorithms for purely asynchronous distributed systems for arbitrary scenarios, where there is no way to guarantee that an asynchronous system can agree in finite time.

CAP Theorem

The CAP theorem was first proposed by Eric Brewer in 1998 and was demonstrated in 2002 in the paper Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-Tolerant Web Services. It proposes three metrics for distributed systems in an asynchronous network model: Consistency, Availability, and Partition Tolerance, with at most two of these three being satisfied simultaneously when a failure occurs.

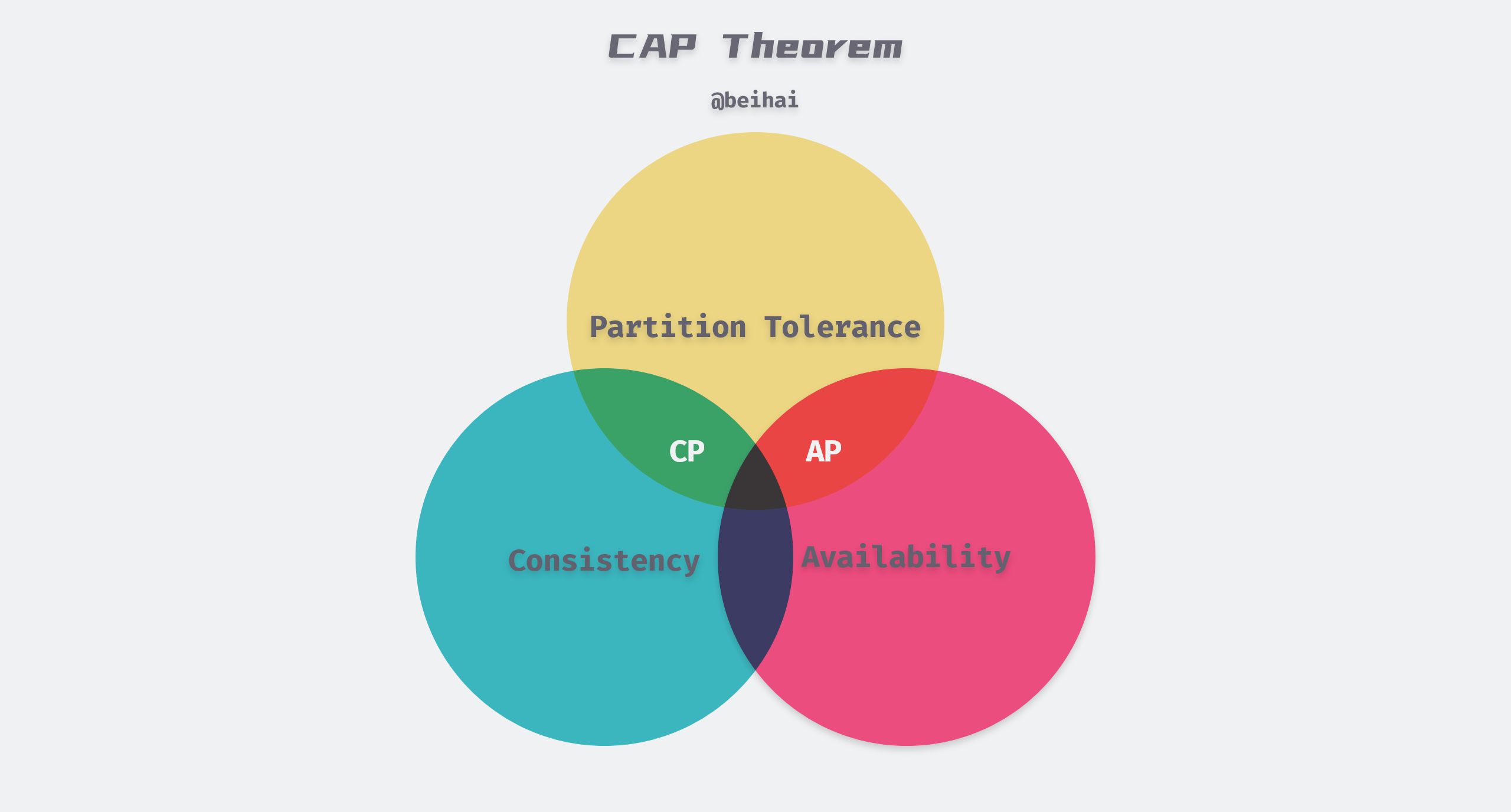
CAP Theorem

  • Consistency: Consistency in CAP theory emphasizes linear consistency (strong consistency), i.e., after a client writes a value to a server and gets a response, it expects to be able to read that value or an updated value from any server, or return an error.
  • Availability: Non-faulty nodes in the system must generate a response to every request received, and servers are not allowed to ignore requests from clients. But availability does not guarantee that the latest written value is read.
  • Partition Tolerance: The system can continue to operate despite the loss or delay of any number of messages on the network between cluster nodes. When a network partition occurs, all messages sent from one node in one partition to a node in another partition are lost.

Most distributed systems are distributed in multiple subnetworks, each of which is called a partition, and each partition has its own communication network and synchronizes data with each other. Network partitioning means that two zones may not be able to communicate with each other, but the nodes are still active.

Since network partitioning is a failure that can happen whether you like it or not, there is no escaping the partitioning problem. When the network is normal, the system can satisfy both consistency and availability, and when there is a network partitioning failure, then there is a trade-off between denying client requests to reduce availability to ensure data consistency, or continuing to provide the service but potentially risking data inconsistency. Therefore, a more accurate description of the CAP theorem is “in the case of network partitioning, choose consistency or availability”.

There is much debate about the CAP theorem, as its definition of availability differs somewhat from the common understanding and considers only one consistency model (linear consistency) and one failure (network partitioning), without considering network latency, node crashes, or other situations that need to be handled. So after this, the BASE theory was proposed.

BASE Theory

The BASE theory is a summary of eBay architects’ practice of large-scale Internet distributed systems, and was published in ACM in [3] Base: An Acid Alternative. The core idea is that even though strong consistency is not possible, but each application can adopt an appropriate approach to make the system ultimately consistent according to its business characteristics.

BASE is the result of a tradeoff between consistency and availability in CAP, and presents three concepts for distributed systems.

  • Basic Availability (Basically Available)
  • Soft State
  • Eventually Consistent

The BASE theory suggests that to achieve horizontal scaling of the system, it is necessary to partition the business functionally and migrate different functional groups of data to mutually independent database servers. Due to the reduced transaction coupling, it is not possible to rely solely on database constraints to ensure consistency between functional groups, and BASE proposes to use message queues to execute decoupled commands asynchronously.

Transactions and Message Queues

In the above figure, the buyer purchases a certain number of items, the order information is recorded in real-time in the transaction table, and subsequent operations that need to be performed are sent to the message queue. At the same time, a separate message processing component, which constantly takes messages from the queue, updates the sales information of a merchant in the user table. In this simple transaction system, the buyer simply waits for the order information to be written and the transaction is completed, and the delay in updating the product sales has no impact on the buyer.

The ultimate consistency emphasized by the BASE theory allows for an intermediate state of data in the system and considers that this state does not affect the overall availability of the system, i.e., allowing for data latency for multiple copies of data from multiple nodes. However, within a certain period of time, all replicas should be guaranteed to have consistent data to achieve the ultimate consistency of data.

Overall BASE theory is oriented to large, highly concurrent, scalable distributed systems.BASE proposes to obtain availability by sacrificing strong consistency and allowing data inconsistency for a short period of time. In practical scenarios, different businesses have different requirements for data consistency, so consistency models such as causal consistency and monotonic read consistency are derived, and the final choice is determined by the usage scenario.

Summary

This section introduces the problems faced by distributed systems and the related theorems, which tell us that when we design and choose a distributed system, we need to develop different solutions for specific needs, and a system oriented to request 1GB data three times per second may be completely different from a system that requests 4KB 1,000 times per second. Therefore, various consensus algorithms are proposed for different usage scenarios, which are described below.

Atomic Commit vs. 2PC

Single-node transactions are atomic in nature. When a transaction containing multiple writes goes awry during execution, atomicity provides very simple semantics for upper-level applications: the result of the transaction is either that all writes are successfully committed, or that the abort operation rolls back everything written. Atomicity prevents failed transactions from polluting the database and creates partial successes interspersed with partial failures.

The atomicity of transactions executed on a single database node is usually the responsibility of the storage engine and relies on the sequential relationship between data persistence writes to disk, i.e., data is written first, then the record is committed. But in a distributed system, it is not enough to simply send a write request to all nodes and then have each node execute the transaction commit independently; it can easily happen that some nodes commit successfully while some others fail.

  • some requests may be lost in the network and eventually discarded due to timeouts.
  • some nodes detect data conflicts or constraint violations and thus decide to abort the operation.
  • Some nodes may crash before committing the record and then roll back on recovery, and eventually the record is discarded.

If some nodes commit a transaction while others drop it, this violates the data consistency guarantee. Moreover, transactions are also isolated and persistent, and the commits of transactions are not visible to each other and cannot be undone. So this requires that if some nodes commit a transaction, then all nodes must follow suit.

2PC

Two Phase Commit (2PC) is a consensus algorithm that implements atomic commit of transactions among multiple nodes to ensure that all nodes either commit or abort. 2PC introduces a new node identity of Coordinator, while other nodes are called Participant, and all requests from the client All requests from clients need to be processed by the coordinator.

2PC divides the transaction commit process into two phases, preparation and commit, in the preparation phase.

  1. the coordinator sends the transaction content to all participants and asks whether the transaction commit can be performed.
  2. the participant nodes execute the transaction operation and then record the Redo and Undo information in the log.
  3. the participants send a response back to the coordinator.

If the participant executes the transaction successfully, then a Yes response is given to the coordinator, and a No response is given in the opposite direction. If the coordinator gets a Yes response from all participants, then the coordinator sends a commit request to all participant nodes to complete the transaction write.

However, if any participant gives a No response, or if the coordinator waits for a timeout and cannot receive feedback from all nodes, the coordinator breaks the transaction and sends a rollback request to all nodes. The participant rolls back the transaction using a phase of Undo logs.

2pc

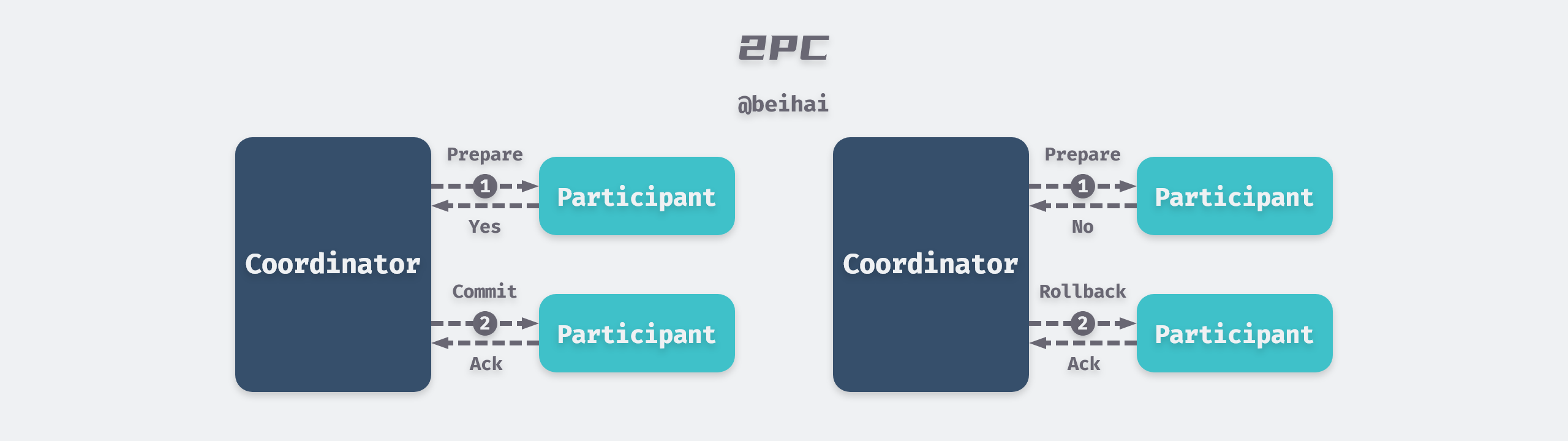
2PC uses distributed transaction IDs to mark requests, which ensures that there are no conflicts between transactions. If a node crashes, the coordinator will retry indefinitely until all nodes agree before continuing to process later requests. 2PC’s synchronization blocking problem greatly limits the overall performance of the system, and the time taken to execute a write request is determined by the ‘slowest’ node in the cluster.

Another major drawback of the 2PC protocol is that all requests must be handled by the coordinator, and participants must wait for the coordinator’s next decision. If the coordinator crashes or has a network failure, participants have no choice but to wait, which can lead to a long period of service unavailability.

coordinator crash

3PC

Three-phase commit improves somewhat on two-phase commit by splitting the preparation process into two phases, forming CanCommit, PreCommit, and DoCommit.

  1. the coordinator sends a CanCommit message to the participant containing the contents of the transaction, and the participant responds with a Yes if it believes it can execute the transaction successfully.
  2. the coordinator sends a PreCommit message to the participant, executes the transaction, and records Redo and Undo information.
  3. the coordinator sends a DoCommit message to perform the transaction commit.

3PC assumes a bounded network delay and that the node can respond within a specified time, so 3PC determines whether the node is faulty by whether the connection times out: if the participant waits for the second stage command to time out, it automatically aborts the transaction, and if it waits for the third stage command to time out, it automatically commits the transaction. Compared to two-phase commit, the biggest advantage of the three-phase commit protocol is that it reduces the blocking range of participants and can continue to be consistent after a single point of failure.

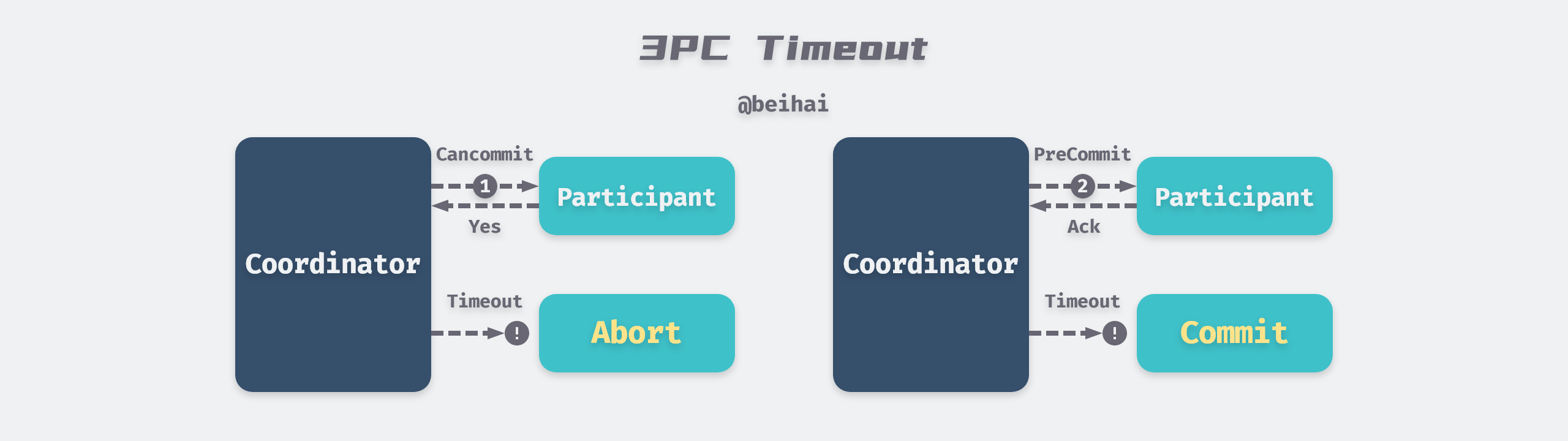
3 pc timeout

3PC introduces new problems while solving single-point blocking. Due to the uncertainty of network latency, it may cause false-death false positives of nodes, e.g., if the coordinator sends an abort message in the third phase but some participants do not receive it in time, then the transaction will be automatically committed, resulting in inconsistent data. In a network environment with infinite latency, the timeout mechanism is not a reliable fault detector, and requests may end up timing out due to network problems even if the node is normal. Therefore 2PC is still commonly used despite the fact that people are aware of some problems with coordinators.

Summary

Normally, the master node in a cluster is very stable, and the 2PC protocol does a good job of atomic commit of distributed transactions, but it does not care about fault tolerance, it forces a node to be the ‘dictator’ and it makes all the decisions. This means that once that node crashes and fails, the system cannot continue to make any decisions. The problem of service unavailability caused by a single point of failure is unacceptable in some scenarios, so a solution that supports fault tolerance is needed.

Consensus to support fault tolerance

In the physical world where computer systems reside, components fail frequently; for example, studies have shown that the average failure-free time of hard disks is about 10 to 50 years, so in a storage cluster containing 10,000 disks, we should expect one disk to fail every day. Since hardware problems cannot be avoided, we need to address failures, and some of the most well-known consensus algorithms that support fault tolerance include Paxos, Raft, Zab, etc., and each of these algorithms is described in this section.

Paxos

Paxos is a theoretical consistency solution proposed by Leslie Lamport in 1990 in his paper [4] The Part-Time Parliament. solution, a paper in which a fictional island called Paxos is used to describe the process by which consensus algorithms solve the data consistency problem.

In ancient Greece, there was an island called Paxos, where a part-time parliament was used to pass decrees, but the member of Paxos did not want to devote his full time to parliamentary affairs. The members of the council passed messages by messenger, but the members and the messenger could leave the council chamber at any time, and the messenger could repeat the message or never return (but not tamper with it). Therefore, the parliamentary agreement should ensure that the decree can continue to be produced even if each deputy may be absent at any time, and that no conflicts will arise.

The problem faced by the part-time parliament corresponds to the problem faced by today’s fault-tolerant distributed systems: the parliamentarians correspond to the processing processes in the distributed system, and the absence of the parliamentarians corresponds to the downtime or network failure of the processing processes. But in this paper, Lamport used a story narrative that made it difficult for many engineers to properly understand the concept of algorithms. So in 2001, Lamport compromised and published Paxos Made Simple, a paper that retells Paxos in easy-to-understand language.

Two specific consensus algorithms, Basic Paxos and Multi-Paxos, are discussed in the Paxos paper, and are described below.

Basic Paxos

In the Paxos algorithm, the cluster has three participating roles, Proposer, Acceptor and Learner, each consisting of multiple processes, and a process can only take one role at a time, but the processes can switch identities. The Learner is just a copy of the data and does not participate in the consensus process.

Each decree proposal in Paxos has its own unique number, and different Proposers choose their own numbers from the set of disjoint numbers, so that no two Proposers will generate proposals with the same number. In Paxos, a proposal is passed if more than half of the nodes write to it, which prevents the slower nodes in the cluster from blocking the response. Also, Paxos ensures that only one proposal can be selected, and that if a proposal is selected, it cannot be modified.

Paxos runs in two phases, Prepare and Accept. When the Proposer receives a request from the client, it enters the following process.

  1. Prepare:

    1. the Proposer selects a proposal number N and broadcasts a Prepare request with number N to the Acceptor.
    2. If Acceptor receives a Prepare request numbered N and N is greater than the number of all Prepare requests it has responded to, then it ensures that it does not respond to any proposal numbered less than N and replies to Proposer with the largest numbered proposal it has passed, if it exists.

  2. Accept:

    1. if the Proposer receives a response from more than half of the Acceptors, then it sends an Accept request containing (N, value), where value is the value of the largest numbered proposal in the received response, or the value sent by the client if all responses do not contain proposals.
    2. if the Acceptor receives an Accept request for a proposal numbered N, it may pass the proposal as long as it has not yet responded to a Prepare request with a number greater than N.

Let’s take a simple example to illustrate how Paxos guarantees consistency across multiple proposals. In the image below, Proposer1 and Proposer2 receive a write request from the client (X=2) and (X=5), respectively. P1 first issues a Prepare and Accept request, and both servers A1 and A2 accept P1’s proposal (X=2). Since the proposal meets the half-write requirement, the proposal is passed by the cluster. After this, P2 sends a Prepare(2.1) request, and since A2 has already accepted (X=2), it returns the accepted proposal number and value (2.1, 2), and P2 uses the received proposal instead of its own to send Accept(2.1, 2) requests to other servers, and eventually all servers agree and choose the same value.

Basic Paxos and Data Consistency

It is important to note that Basic Paxos can only form a consensus for one value, and once a proposal is determined, the value will never change, meaning that the entire Paxos set will only accept one proposal.

There is an extreme case of Basic Paxos. Imagine if P1 proposes proposal number N1 and completes the preparation phase successfully, and then P2 proposes proposal number N2 and also completes the preparation phase, then Acceptor ignores P1’s Accept request. P1 then enters the preparation phase again and proposes proposal number N3, and so on, which results in both proposals not being selected.

Although one Proposer wins in the end due to network delays or node failures, the proposal ‘deadlock’ consumes a lot of time and network resources, which is solved in Multi-Paxos.

Multi-Paxos

Multi-Paxos is a modification of Basic Paxos. To avoid proposals from getting stuck in the dead-end loop mentioned above, Multi-Paxos elects a master Proposer (called the Leader), which makes all proposals, and the other Proposers forward client requests to the master Proposer. As long as the Leader can communicate with more than half of the Acceptors, it can keep advancing the proposal numbers, and the proposals will eventually be approved.

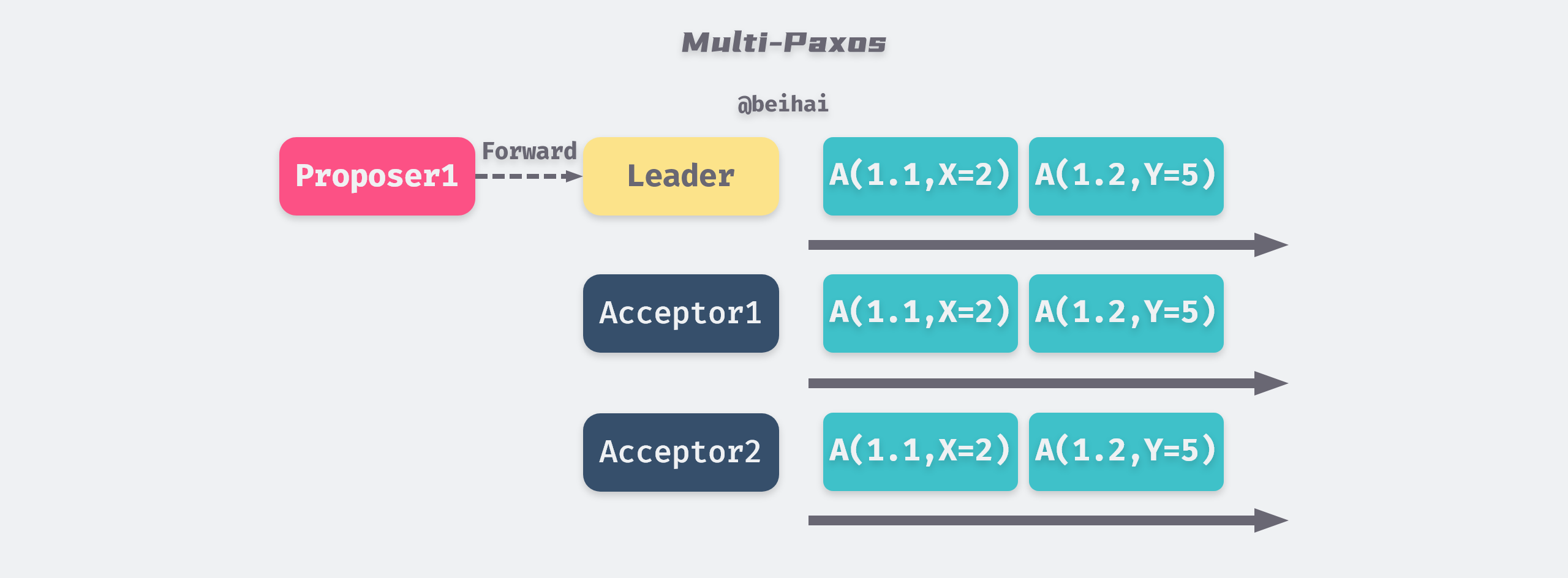
Multi-Paxos

Multi-Paxos does not have any restrictions on the election process, any node can be elected as Leader, so after the new Leader is elected, it needs to synchronize with other Acceptors first. If the new master node is behind in data, it will take a longer time to synchronize the data.

In fact, Lamport’s paper does not describe exactly how the Leader should be elected, nor does it describe in detail how to handle some boundary conditions, which makes each Paxos algorithm implementation more or less different.

Raft and Zab

Raft and Zab are both based on Multi-Paxos, which simplifies the algorithm model and makes it easier to understand; Zab is an atomic broadcast protocol designed especially for ZooKeeper to support crash recovery, while Raft is a general distributed consensus algorithm, the core ideas of these two algorithms are basically the same, so we mainly use Raft as an example.

A Raft cluster contains several server nodes, each of which has a unique identification ID and is in one of the three states Leader, Follower, Candidate at any given moment. In general, there is only one Leader in the system and all other nodes are Follower. If the Follower does not receive a message from the Leader within a certain period of time, it becomes Candidate and initiates an election, and the candidate with the majority of votes (more than n/2+1) in the cluster becomes the new Leader.

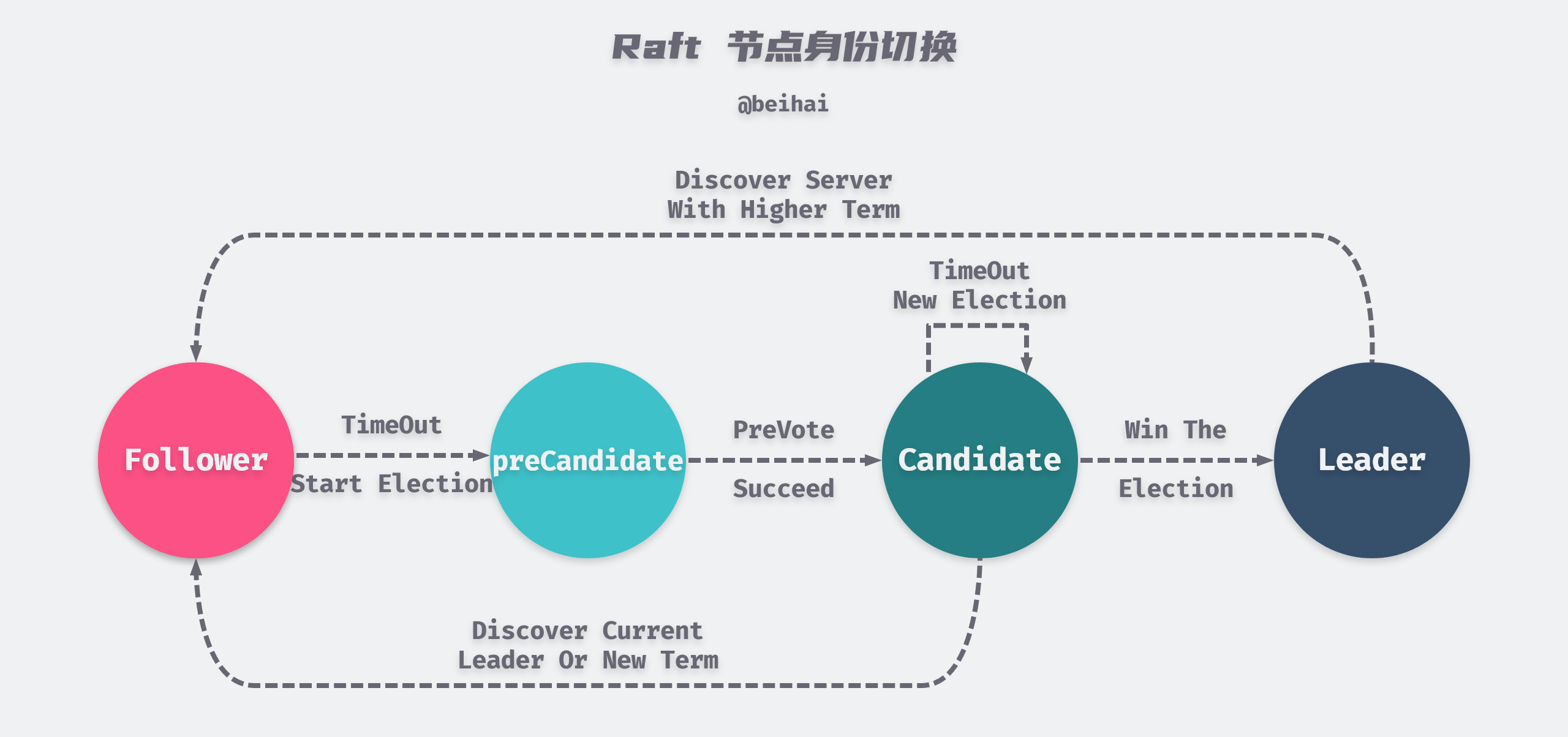
Raft node identity switching

The election process can be clearly seen in the image above, and Raft imposes some restrictions on the election process. First, before launching an election, candidates need to try to connect to other nodes in the cluster and ask them if they are willing to participate in the election, and if other nodes in the cluster can receive heartbeat messages from the Leader properly, then they will refuse to participate in the election. Second, only the node with the most up-to-date and complete logs can be elected Leader.

The pre-voting mechanism prevents outlying nodes from frequently refreshing their tenure values and prevents the node from rejoining the cluster with a larger tenure value to depose the Leader.

Raft uses a global clock to ensure that all write operations are linear, and that any data replica in the cluster performs the same sequence of commands as requested by the client, i.e., given a sequence of requests, the data replicas always perform the same internal state transitions and produce the same responses, even if the replicas are received in a different order.

Raft is widely used in the industry, with distributed databases like etcd and TiDB built on Raft, and Redis6 adding the Raft module to ensure data consistency, so it is a safe decision to prioritize Raft in your project. For more detailed information on Raft implementation, you can read the paper In Search of an Understandable Consensus Algorithm (Extended Version).

Summary

All the algorithms in this section can be summarized as Paxos-like algorithms, and their consensus process is very similar to two-phase commit. The major difference is that the master node of 2PC is externally designated, while the Paxos-like algorithm can re-elect a new master node and enter the consensus state after the master node crashes and fails. In addition, the fault-tolerant consensus algorithm can pass a resolution as long as it receives a majority vote from the nodes, while 2PC requires a Yes response from each participant to pass. These differences are key to ensure the correctness and fault-tolerance of the consensus algorithm.

Finally, it is important to emphasize that the Paxos-like algorithm supports fault tolerance provided that the number of nodes that crash or become unavailable is less than half of the nodes, so that at least one surviving node has the most up-to-date and complete data and no data loss occurs.

Byzantine Fault Tolerance

So far, all of this paper assumes that nodes are unreliable but necessarily honest, that nodes will not maliciously send incorrect messages, and that messages will not be tampered with on the way to sending. The blockchain technology, which was relatively popular in the previous years, is one of the main selling points for tamper-proofing, which further extends the scope of fault tolerance in distributed systems and brings the related theoretical knowledge to the public. This class of algorithms is collectively known as Byzantine fault-tolerant algorithms.

The Byzantine Generals Problem

In 1982, Lamport published a paper The Byzantine Generals Problem with Robert Shostak and Marshall Pease, proposing Byzantine Generals Problem to describe the phenomenon of message unreliability in distributed systems. This paper is still narrated as a story narrative.

A group of Byzantine generals each leads an army to jointly besiege a city, and the action strategy of each army is limited to either attack or retreat. Because of the potentially disastrous consequences of some armies attacking and some armies retreating, the generals must vote to agree on a strategy of all armies attacking together or all armies retreating together. The generals are located in different directions of the city, and they can only communicate with each other by messenger. During the voting process, each general informs all the other generals via messenger of his vote to attack or retreat, so that each general knows the common outcome of his vote and the information sent by all the other generals and decides on a strategy.

The problem with this system is that there can be traitors among the generals and messengers who may not only vote for the worse strategy, but may also selectively send their votes.

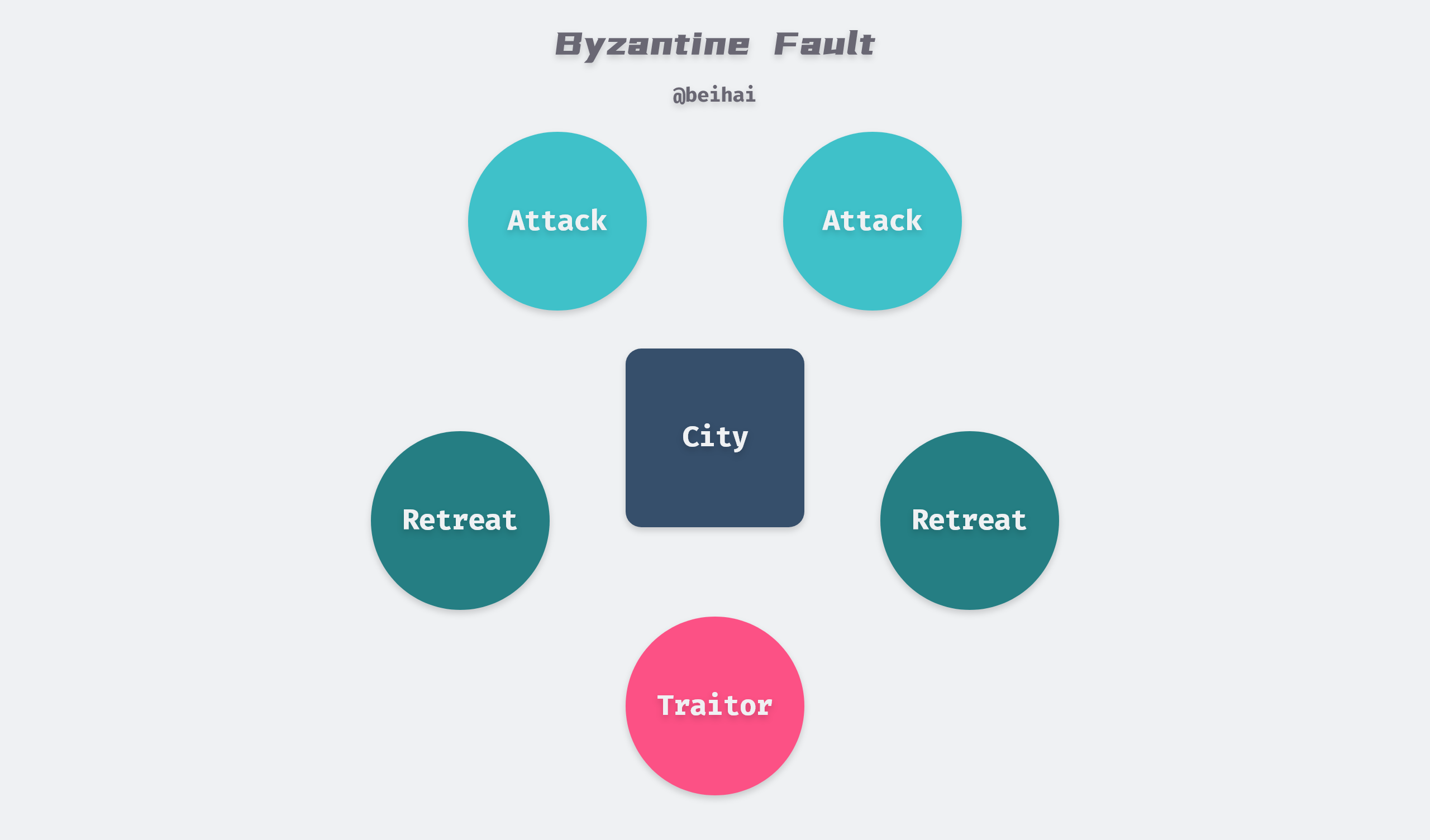
Byzantine fault

For example, in the picture above, let’s assume that there are 5 generals voting and 1 of them is a traitor. 2 of the 4 loyal generals vote to attack and 2 vote to withdraw. The traitor may have deliberately sent a letter to the 2 offensive generals indicating that he voted offensive, and a letter to the 2 evacuation generals indicating that he voted evacuation.

This results in a situation where in the opinion of the 2 generals who voted for the offense: the vote results in 3 people voting for the offense and thus launching the offense, while in the opinion of the 2 generals who voted for the withdrawal: the vote results in 3 people voting for the withdrawal. Thus the concerted synergy of the armies is broken.

Byzantine fault tolerance is to ensure that honest generals follow the principle of majority rule in case of traitor interference, and that honest nodes can also reach consensus. lamport proved in his paper that if the number of malicious nodes is m, consensus can be ensured as long as the total number of nodes can reach 3m+1. In other words, for consensus to be reached successfully, at least 2/3 of the nodes in the system must be guaranteed to be honest.

POW and POS

The Proof-of-Work (POW) concept was introduced in 1993 by Cynthia Dwork and Moni Naor, and was initially used to stop DDOS attacks and spam, among other service abuse problems. Today this algorithm has been given a new meaning in the form of ‘mining’ as the core of Bitcoin, helping the cluster to elect a leader to decide the content of the next block.

POW requires each node to perform some appropriately time-consuming problem solving before executing the request, a problem that is hard to find a solution to, but easy to verify the correctness of the answer, and the first node to compute the result is given bookkeeping rights (data writing rights) and broadcasts the data to other nodes for verification. In the Bitcoin network, the problem becomes increasingly difficult to solve, ensuring that the master node is switched about once every 10 minutes to prevent the current node from ‘defecting’.

POW and POS

The most common computation for problem solving is Hash, e.g. given a sequence of characters, it is required to add a random number to the sequence so that the first four bits of the result of the SHA-256 hash function are all 0. The node computes the required value by exhaustive guessing, and only one Hash operation is required for verification.

1

SHA256(Hello World107105) == 0000bfe6af4232f78b0c8eba37a6ba6c17b9b8671473b0b82305880be077edd9

Because problem solving is a purely probabilistic event, the more attempts you make the higher the probability of getting an answer, the POW algorithm favors nodes with more computational power and a better network environment to be elected as master nodes. This has led to the creation of massive mining pools in the Bitcoin network that waste a lot of computing power and electricity in order to get the bookkeeping reward.

In 2011, a user posted a thread in the Bitcoin forum Proof of stake instead of proof of work , proposing the proof-of-stake (POS) , the concept of POS). Proof of stake removes the energy and computational power requirements of proof of work, and replaces them with equity. Each node uses its own digital currency holdings as ’equity’ collateral, and the next holder of bookkeeping rights is chosen randomly based on the shares and time of different nodes.

Since the probability of a node being elected is positively correlated with the percentage of pledged equity, this gives richer nodes more chances to get bookkeeping rights, and it is difficult for small shareholders to do anything with a few thousandths or even ten thousandths of shares. The improved Delegated Proof-of-Stake (DPOS) enables nodes to delegate their stakes to an agent to compete for bookkeeping rights on their behalf, so that minority shareholders can also reap the benefits.

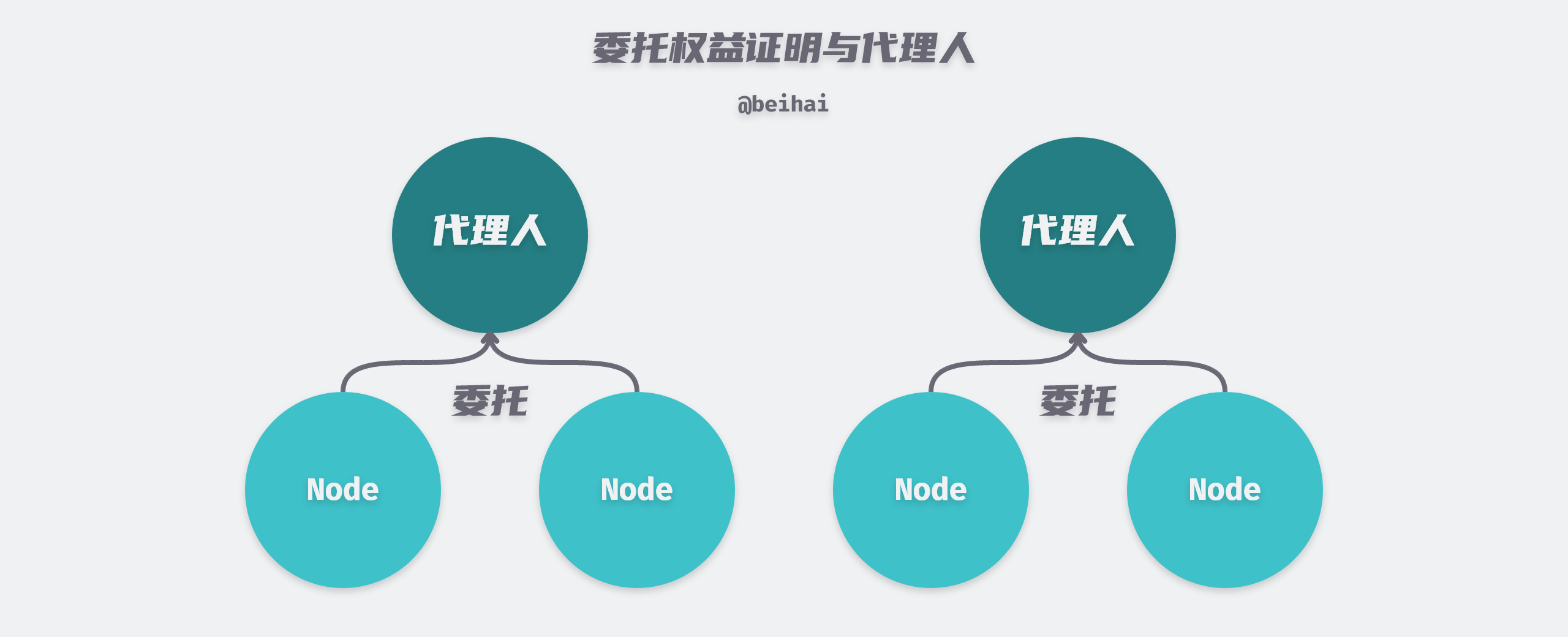
Certificate of Entrusted Interest and Agent

In the delegated proof of interest, each participant can elect any number of nodes to compete for the bookkeeping rights, and the top N nodes with the most votes become the candidates, and the next bookkeeping right holder is chosen randomly from such a set of candidates. In addition, the number of N is also determined by the entire network vote, which ensures the randomness of the election as much as possible.

As the two most important consensus algorithms in blockchain, POW and POS both introduce the concept of economics, which can eliminate the attacker’s motivation and ensure the interests of the majority by making the cost of attack much higher than the benefit and very expensive. For students interested in blockchain consensus, you can watch the video Proof-of-Stake (vs proof-of-work) which introduces the differences, advantages and disadvantages of POW and POS in more detail.

Summary

Byzantine fault tolerance is the most stringent consensus in distributed systems. In addition to the well-known blockchain, some instant systems with high security requirements such as Boeing’s flight control system and SpaceX also adopt Byzantine fault tolerance consensus algorithm. However, for most of the systems, they are deployed in a LAN environment and message tampering is very rare; on the other hand, the problem of incomplete messages due to network reasons can be avoided using the checksum algorithm, so if the environment is trustworthy, Byzantine fault is not considered in most cases.

At present, there are not many Byzantine fault tolerance application scenarios, and I have considered whether I should add this aspect when finishing this article. From a general point of view, Byzantine fault tolerance is currently the highest level of fault tolerance, and can even solve the circuit errors that occur when computers run in distributed environments (there is no way to simply use cryptography and digital signatures to avoid), understanding this knowledge may bring a different way to solve the problem.

Summary

This article first introduces some important theories, including the FLP impossibility theorem, which states that one should not design a general consensus algorithm for asynchronous distributed systems and that a ‘silver bullet’ does not exist, and the CAP and BASE theories, which discuss some application-specific scenarios. The article summarizes three types of consensus algorithms: 2PC and its variant 3PC, which implements atomic commit, Paxos, which supports fault tolerance, and POW and POS, which solve the Byzantine general problem. it is easy to see that scalability is not the only reason to use a distributed system, but fault tolerance and low latency are also important goals. How to choose a consensus algorithm that better meets your needs is a far-reaching decision.

In addition, the above consensus algorithms have a common feature: they use master-slave replication to improve the scalability of the system, so how to choose the master and how to synchronize the data is their common thinking when solving the problem, perhaps in the project will focus on the maintenance of the “master-slave replication” point will have different gains.

There are still many problems to be solved in the distributed space, and dealing with them is not only an ongoing active area of research, but also a major concern when building practical distributed systems; slowing down and gaining more knowledge is not a bad thing after all.

Reference