Cons, an interesting data structure

Preface

There is an interesting data structure in lisp, Cons, which uses function closures to encapsulate a two-tuple data structure and build any other data structure needed on top of that. Before this, although I knew about closures and such, and had written some higher-order functions, I hadn’t thought about the possibility of using functions to build data structures, and I’ll explain how to do that in ts below.

lisp cons’s wiki

The basic definition is as follows.

$$ c=cons(a,b)
car(c)=a
cdr(c)=b $$

Initial Implementation

The cons initial implementation is simple and can be implemented in just a few lines of code. As you can see, it simply binds the arguments a and b using closures and returns them when the function is executed.

function cons(a: number, b: number): (n: number) => number {
  return (n: number) => (n === 0 ? a : b);
}
function car(cons: (n: number) => number) {
  return cons(0);
}
function cdr(cons: (n: number) => number) {
  return cons(1);
}

It can be used in the following way.

1
2
3

const n = cons(1, 2);
console.log(car(n)); // 1
console.log(cdr(n)); // 2

To make it look a little more practical, first supplement its type with a generic type.

export interface Cons<A, B> {
  (s: 0): A;
  (s: 1): B;
  _0: A;
  _1: B;
}

export function cons<A, B>(a: A, b: B): Cons<A, B> {
  return ((s: 0 | 1) => (s === 0 ? a : b)) as any;
}
export function car<T extends Cons<any, any>>(cons: T): T["_0"] {
  return cons(0);
}
export function cdr<T extends Cons<any, any>>(cons: T): T["_1"] {
  return cons(1);
}

Verify it using the following unit tests.

it("cons", () => {
  const c = cons("hello", 1);
  expect(car(c) as string).toBe("hello");
  expect(cdr(c) as number).toBe(1);
});

It doesn’t look like much use. But it will be used below (the simplest binary structure) to combine into more complex data structures such as chains and trees.

Linked list

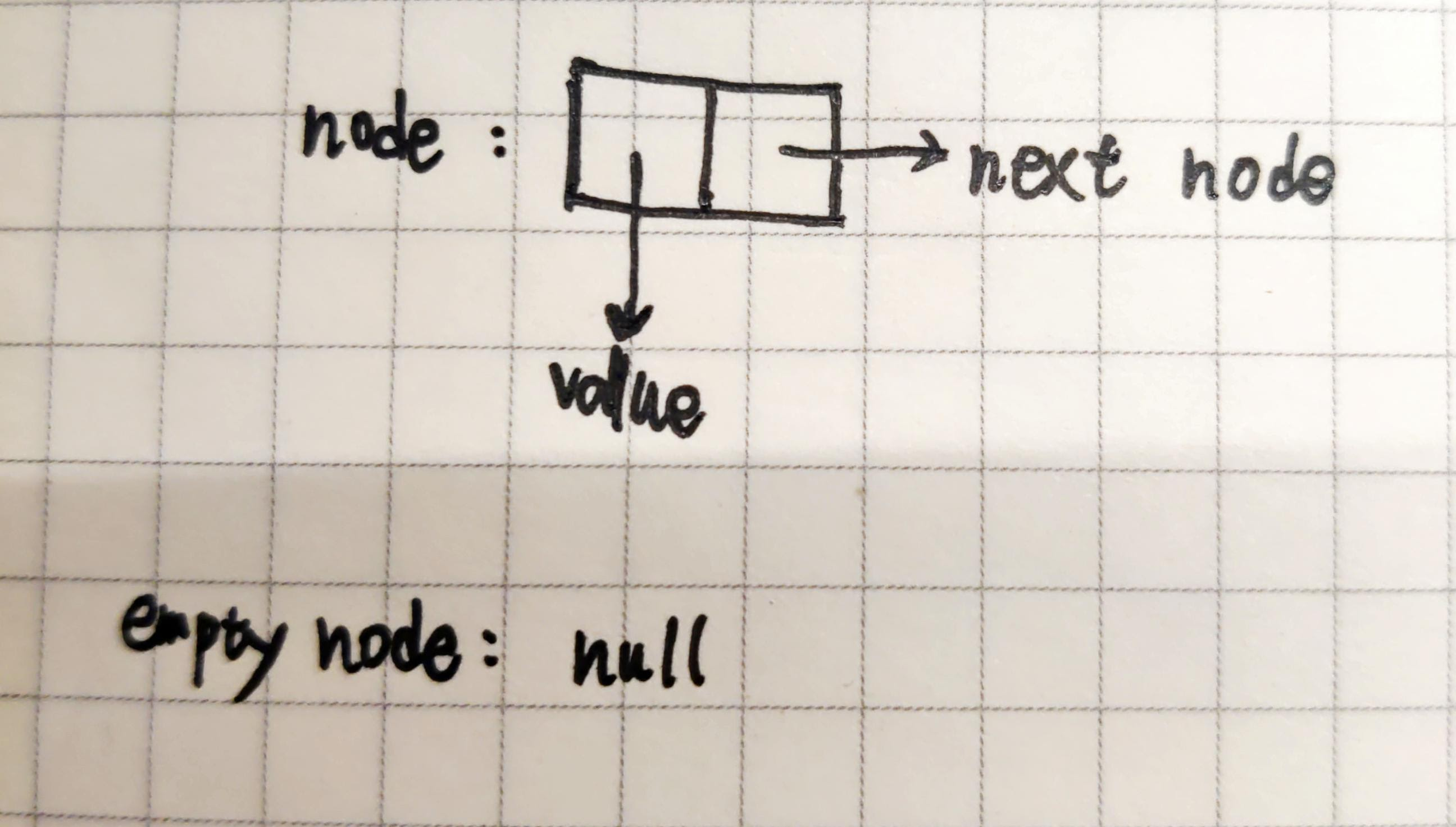
In fact, once you have a binary, you can go on to combine any data structure you need, and a Linked list is a simple example of this. Here the car part of cons stores the value of the current node in the Linked list, and cdr stores a pointer to the next node.

Linked list

type List<T> = Cons<T, List<T>> | null;
function list(): null;
function list<T>(...args: T[]): Exclude<List<T>, null>;
function list<T>(...args: T[]): List<T> {
  function iter(i: number): List<T> {
    return i === args.length ? null : cons(args[i], iter(i + 1));
  }
  return iter(0);
}

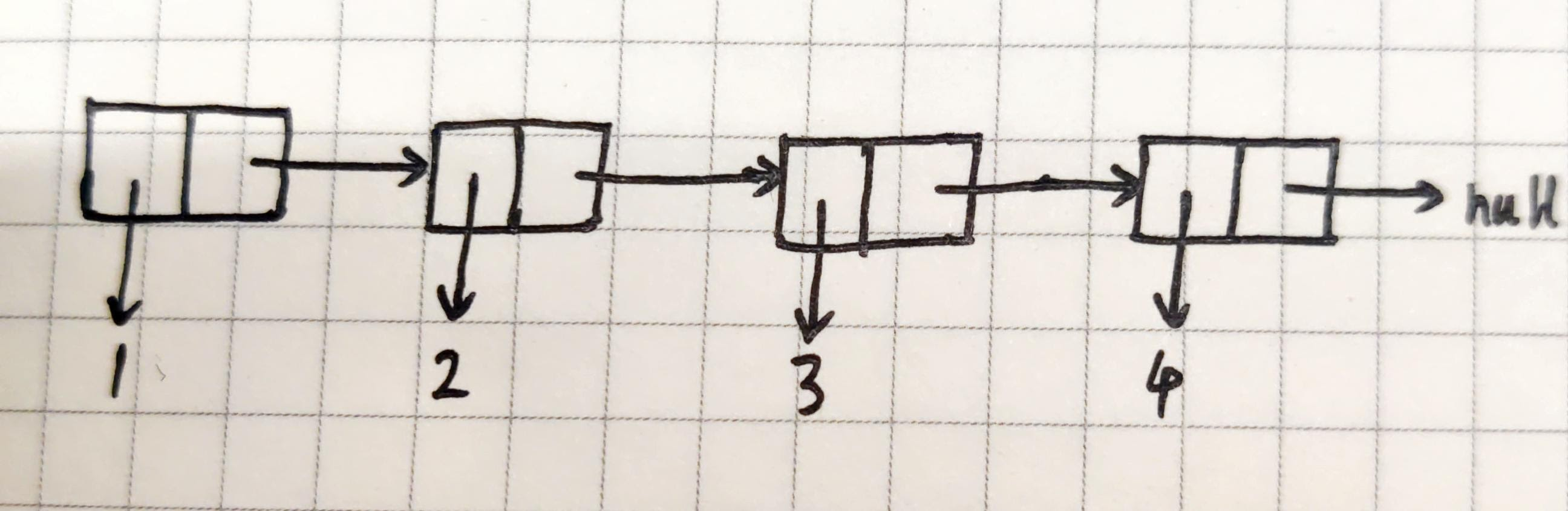
The following is a Linked list that stores 4 elements.

`1`	`list(1, 2, 3, 4);`

It will be a cons nested call procedure.

`1`	`cons(1, cons(2, cons(3, cons(4, null))));`

Linked list

You can write map/filter/reduce functions for it.

map/filter is nothing complicated, just recursive processing of each node.

function map<T, R>(list: List<T>, f: (i: T) => R): List<R> {
  return list === null ? null : (cons(f(car(list)), map(cdr(list)!, f)) as any);
}
function filter<T>(list: List<T>, f: (i: T) => boolean): List<T> {
  return list === null
    ? null
    : f(car(list))
    ? cons(car(list), filter(cdr(list), f))
    : filter(cdr(list), f);
}

The following is a schematic diagram of processing using map.

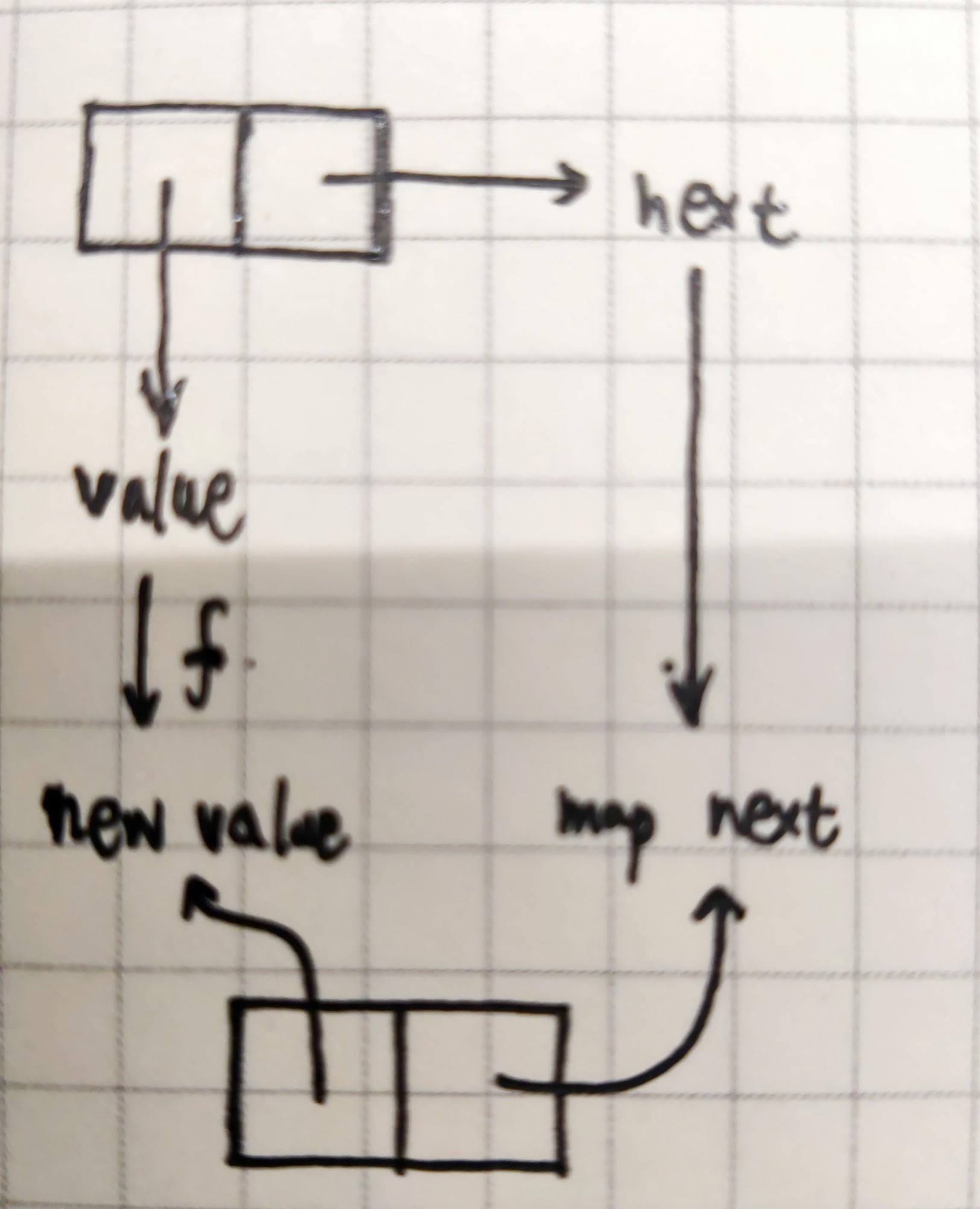
processing

reduce will be a little special in that it is an iterative recursion.

function reduce<T>(list: List<T>, f: (res: T, v: T, i: number) => T): T;
function reduce<T, R>(
  list: List<T>,
  f: (res: R, v: T, i: number) => R,
  init: R
): R;
function reduce<T, R>(
  list: List<T>,
  f: (res: R, v: T, i: number) => R,
  init?: R
): R {
  function iter(list: List<T>, init: R, i: number): R {
    return list === null
      ? init
      : iter(cdr(list)!, f(init, car(list), i), i + 1);
  }
  return init !== undefined
    ? iter(list, init, 0)
    : iter(cdr(list!), car(list!) as unknown as R, 1);
}

It can be used in the following ways.

const res = reduce(
  map(
    filter(list(1, 2, 3, 4), (i) => i % 2 === 0),
    (i) => i * 2
  ),
  (a, b) => a + b,
  0
);
console.log(res); // 12

In theory, it should be easy to convert map/filter to a higher-order function based on reduce, such as the following code which implements map/filter based on reduce in js.

function map<T, R>(list: T[], f: (i: T) => R): R[] {
  return list.reduce((res, i) => {
    res.push(f(i));
    return res;
  }, [] as R[]);
}
function filter<T>(list: T[], f: (i: T) => boolean): T[] {
  return list.reduce((res, i) => {
    if (f(i)) {
      res.push(i);
    }
    return res;
  }, [] as T[]);
}

If one wishes to base the map/filter implementation of the Linked list here on reduce, this is currently not possible. Note that the above code uses push, which is a modify operation that is more recommended for immutable state in functional programming. So, is there some way to do this without changing the state? I will try to implement it.

function concat<T>(a: List<T>, b: List<T>): List<T> {
  return a === null ? b : cons(car(a), concat(cdr(a), b));
}
function mapForReduce<T, R>(arr: List<T>, f: (i: T) => R): List<R> {
  return reduce(arr, (res, i) => concat(res, list(f(i))), null as List<R>);
}
function filterForReduce<T>(arr: List<T>, f: (i: T) => boolean): List<T> {
  return reduce(
    arr,
    (res, i) => (f(i) ? concat(res, list(i)) : res),
    null as List<T>
  );
}

Of course, someone might say: Isn’t it inefficient to link two Linked lists each time you iterate over an element? Yes, it is, so there is another, slightly more bizarre, method that can be used.

function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
  return reduce(
    list,
    (res, i) => {
      return i === null ? res : (next) => res(cons(f(i), next));
    },
    (r: List<R>) => r
  )(null);
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
  return reduce(
    list,
    (res, i) => (f(i) ? (next) => res(cons(i, next)) : res),
    (r: List<T>) => r
  )(null);
}

Admittedly, this approach does not seem to accumulate a stack on each recursion, but it also wraps the res function over and over, eventually calling it all at once by passing a single argument at the end of reduce, which does not solve the fundamental problem, so the following implementation of setCar/setCdr.

Support for modifying car/cdr

To implement set, you actually have to modify the parameters of the closure binding.

export interface Cons<A, B> {
  (s: "car"): A;
  (s: "cdr"): B;
  (s: "setCar"): (v: A) => void;
  (s: "setCdr"): (v: B) => void;
  _0: A;
  _1: B;
}

export function cons<A, B>(a: A, b: B): Cons<A, B> {
  return ((s: string) =>
    s === "car"
      ? a
      : s === "cdr"
      ? b
      : s === "setCar"
      ? (v: A) => (a = v)
      : (v: B) => (b = v)) as any;
}
export function car<T extends Cons<any, any>>(cons: T): T["_0"] {
  return cons("car");
}
export function cdr<T extends Cons<any, any>>(cons: T): T["_1"] {
  return cons("cdr");
}
export function setCar<T extends Cons<any, any>>(cons: T, v: T["_0"]): void {
  return cons("setCar")(v);
}
export function setCdr<T extends Cons<any, any>>(cons: T, v: T["_1"]): void {
  return cons("setCdr")(v);
}

This can be verified using the following unit tests.

it("cons", () => {
  const c = cons("hello", 1);
  expect(car(c) as string).toBe("hello");
  expect(cdr(c) as number).toBe(1);
  setCar(c, "liuli");
  setCdr(c, 2);
  expect(car(c) as string).toBe("liuli");
  expect(cdr(c) as number).toBe(2);
});

However, an alternative implementation is proposed in the course, which is implemented entirely using higher-order functions and does not use internal judgments in cons.

export interface Cons<A, B> {
  (m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any): any;
  _0: A;
  _1: B;
}

export function cons<A, B>(a: A, b: B): Cons<A, B> {
  return ((
    m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any
  ) =>
    m(
      a,
      b,
      (n: A) => (a = n),
      (n: B) => (b = n)
    )) as any;
}
export function car<T extends Cons<any, any>>(cons: T): T["_0"] {
  return cons((a) => a);
}
export function cdr<T extends Cons<any, any>>(cons: T): T["_1"] {
  return cons((_a, b) => b);
}
export function setCar<T extends Cons<any, any>>(
  cons: T,
  value: T["_0"]
): void {
  cons((_a, _b, setA) => setA(value));
}
export function setCdr<T extends Cons<any, any>>(
  cons: T,
  value: T["_1"]
): void {
  cons((_a, _b, _setA, setB) => setB(value));
}

Now, re-implement mapForReduce/filterForReduce.

function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
  const init = cons(null, null) as unknown as List<R>;
  reduce(
    list,
    (curr, i) => {
      const next = cons(f(i), null) as List<R>;
      setCdr(curr!, next);
      return next;
    },
    init
  );
  return cdr(init!);
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
  const init = cons(null, null) as unknown as List<T>;
  reduce(
    list,
    (curr, i) => {
      if (!f(i)) {
        return curr;
      }
      const next = cons(i, null) as List<T>;
      setCdr(curr!, next);
      return next;
    },
    init
  );
  return cdr(init!);
}

For the code mapForReduce(list(1, 2, 3, 4), i => i) the iterative process is plotted.

i	curr	init
1	(null, null)	(null, null)
2	(1, null)	(null, (1, null))
3	(2, null)	(null, (1, (2, null)))
4	(3, null)	(null, (1, (2, (3, null))))
return		(null, (1, (2, (3, (4, null)))))

As you can see, each time the previous node is modified and the current value is used to construct a new node with cons as the next iteration value, the entire list is eventually traversed and a copy of the entire list is made.

Trees

Since you can construct a Linked List via cons, you can naturally construct a tree structure as well, just by defining a tree structure.

A node is composed of a value and possible children, so we define a tree node this way.

`1`	`cons(value, list(sub1, sub2, ...subN));`

tree

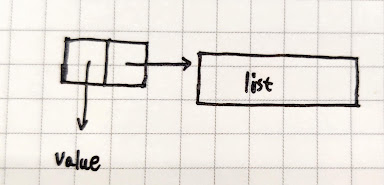
Very simple to implement.

type Tree<T> = Cons<T, List<Tree<T>>>;
function tree<T>(value: T, children: List<Tree<T>> = null) {
  return cons(value, children);
}

const t = tree(1, list(tree(2, list(tree(3))), tree(4)));
expect(car(t)).toBe(1);
expect(car(car(cdr(t)!))).toBe(2);

It is also possible to implement map/filter/reduce for tree structures, as you can see the previous implementations are simple list-based map/filter implementations.

function treeReduce<T, R>(tree: Tree<T>, f: (r: R, v: T) => R, init: R): R {
  init = f(init, car(tree));
  map(cdr(tree), (i) => {
    init = treeReduce(i, f, init);
  });
  return init;
}
function treeMap<T, R>(tree: Tree<T>, f: (v: T) => R): Tree<R> {
  return cons(
    f(car(tree)),
    map(cdr(tree)!, (i) => treeMap(i, f))
  );
}
function treeFilter<T>(tree: Tree<T>, f: (v: T) => boolean): Tree<T> | null {
  if (!f(car(tree))) {
    return null;
  }
  return cons(
    car(tree),
    filter(
      map(cdr(tree)!, (i) => treeFilter(i, f)!),
      (i) => i !== null
    )
  );
}

Test it.

const t = tree(1, list(tree(2, list(tree(3))), tree(4)));
it("basic", () => {
  expect(car(t)).toBe(1);
  expect(car(car(cdr(t)!))).toBe(2);
});
it("treeReduce", () => {
  expect(treeReduce(t, (r, i) => [...r, i], [] as number[])).toEqual([
    1, 2, 3, 4,
  ]);
});
it("treeMap", () => {
  expect(
    treeReduce(
      treeMap(t, (i) => i * 2),
      (r, i) => [...r, i],
      [] as number[]
    )
  ).toEqual([1, 2, 3, 4].map((i) => i * 2));
});
it("treeFilter", () => {
  const res = treeFilter(t, (i) => i % 2 === 1);
  expect(treeReduce(res!, (r, i) => [...r, i], [] as number[])).toEqual([1]);
});

Conclusion

lisp is a seemingly simple language, because it seems to be all about expressions, and it doesn’t offer as many ways to construct complex data (like object objects, structs, classes, etc.) as modern languages. But as you can see here, it is possible to construct arbitrarily complex data structures by supporting the simplest complex data, and the building blocks of all complex data are so simple as to be unbelievable.

Table of Contents

Preface

Initial Implementation

Linked list

Support for modifying car/cdr

Trees

Conclusion