VictoriaMetrics’ vmstorage component receives metrics passed upstream, and in real-world scenarios, the order of magnitude of metrics or transient metrics can be so horrific that if the size of the cache is not limited, there is a risk of excessive slow inserts due to cache misses.

vmstorage

For this purpose, vmstorage provides two parameters: maxHourlySeries and maxDailySeries, which are used to limit the unique series added to the cache per hour/day. uniqueSeries means a unique time series, such as metrics{label1="value1",label2="value2"} belonging to a time series.

But multiple metrics with different values {label1="value1",label2="value2"} belong to the same time series. victoriaMetrics uses the following way to get the unique identifier of the time series.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func getLabelsHash(labels []prompbmarshal.Label) uint64 {
 bb := labelsHashBufPool.Get()
 b := bb.B[:0]
 for _, label := range labels {
  b = append(b, label.Name...)
  b = append(b, label.Value...)
 }
 h := xxhash.Sum64(b)
 bb.B = b
 labelsHashBufPool.Put(bb)
 return h
}

Speed limiter initialization

VictoriaMetrics uses a speed limiter-like concept to limit the number of new unique sequences added per hour/day, but unlike a normal speed limiter, it requires a limit at the sequence level, i.e., it determines whether a sequence is a new unique sequence, and if so, it further determines whether the number of new sequences in the cache over a period of time exceeds the limit, rather than simply at the request level.

1
2

hourlySeriesLimiter = bloomfilter.NewLimiter(*maxHourlySeries, time.Hour)
dailySeriesLimiter = bloomfilter.NewLimiter(*maxDailySeries, 24*time.Hour)

The following is a function to create a new speed limiter, pass in a maximum (sequence) value, and a refresh time. In this function you will.

  1. initialize a goroutine with a maximum number of elements as maxItems.

  2. enable a goroutine that will reset the limiter when the time reaches refreshInterval.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

func NewLimiter(maxItems int, refreshInterval time.Duration) *Limiter {
 l := &Limiter{
  maxItems: maxItems,
  stopCh:   make(chan struct{}),
 }
 l.v.Store(newLimiter(maxItems)) //1
 l.wg.Add(1)
 go func() {
  defer l.wg.Done()
  t := time.NewTicker(refreshInterval)
  defer t.Stop()
  for {
   select {
   case <-t.C:
    l.v.Store(newLimiter(maxItems))//2
   case <-l.stopCh:
    return
   }
  }
 }()
 return l
}

The limiter has only one core function Add, when vmstorage receives an indicator, it will calculate the unique identifier (h) of the indicator by getLabelsHash, and then call the following Add function to determine whether the unique identifier exists in the cache.

If the number of elements currently stored is greater than or equal to the maximum allowed, a filter is used to determine whether the element already exists in the cache; otherwise the element is added directly to the filter, and the element is subsequently allowed to be added to the cache.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func (l *Limiter) Add(h uint64) bool {
 lm := l.v.Load().(*limiter)
 return lm.Add(h)
}

func (l *limiter) Add(h uint64) bool {
 currentItems := atomic.LoadUint64(&l.currentItems)
 if currentItems >= uint64(l.f.maxItems) {
  return l.f.Has(h)
 }
 if l.f.Add(h) {
  atomic.AddUint64(&l.currentItems, 1)
 }
 return true
}

The above filter is a Bloom filter with the core functions Has and Add, which are used to determine if an element exists in the filter and to add the element to the Bloom filter, respectively.

The initialization functions of the filter are as follows. bitsPerItem is a constant with a value of 16. bitsCount counts the total number of bits in the filter, and each bit indicates the existence of a value. bits is measured in 64-bit units (later called slots, for fast retrieval of the target bit in bitsCount). The reason for adding 63 to the calculation of bits is to round up, for example, when maxItems=1, at least 1 unit64 slot is needed.

1
2
3
4
5
6
7
8

func newFilter(maxItems int) *filter {
 bitsCount := maxItems * bitsPerItem
 bits := make([]uint64, (bitsCount+63)/64)
 return &filter{
  maxItems: maxItems,
  bits:     bits,
 }
}

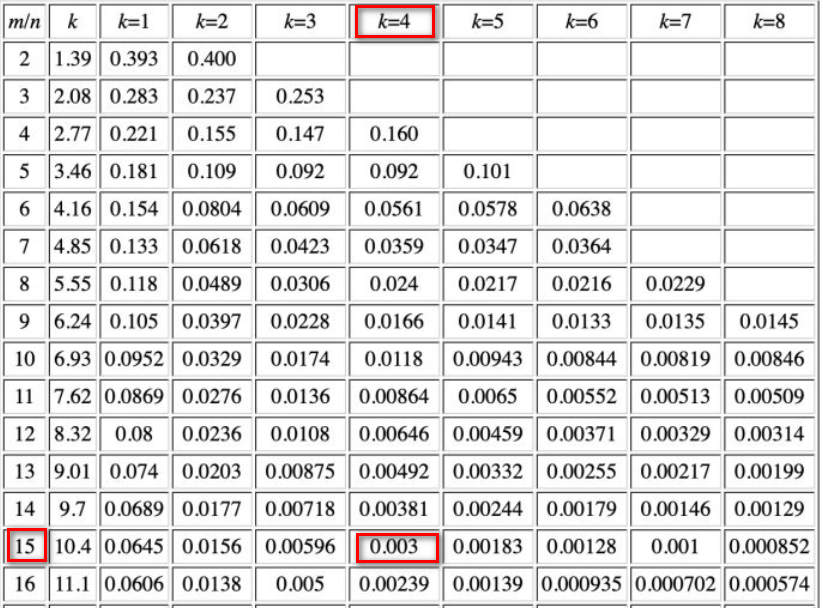
Why bitsPerItem is 16? In this code, k is 4 ( hashesCount ), and the expected miss rate is 0.003 (which can be seen from the official filter_test.go), then the ratio of total storage to total elements is required to be 15, and to facilitate the retrieval of slot (64bit, a multiple of 16), it is set to 16.

1
2
3

if p > 0.003 {
  t.Fatalf("too big false hits share for maxItems=%d: %.5f, falseHits: %d", maxItems, p, falseHits)
}

Bloom filter

The following is the Add operation of the filter, the purpose of which is to add a certain element to the filter. Instead of using multiple hash functions to calculate the hash of an element, the Add function changes the value of the same element and then applies the same hash function to the corresponding value, with the number of element changes limited by hashesCount.

  1. get the complete storage of the filter and convert it to bit units
  2. convert the elements h to byte arrays for xxhash.Sum64 calculation
  3. perform hashesCount to reduce the miss rate
  4. compute the hash of element h
  5. increment the element h to prepare for the next hash
  6. get the bit range of the element by remainder method
  7. get the slot where the element is located (i.e., the bit range of uint64 size)
  8. get the bit of the slot in which the element is located, a bit of 1 means the element exists, a bit of 0 means the element does not exist
  9. get the mask of the bit where the element is located
  10. load the value of the slot where the element is located
  11. if the result of w & mask is 0, the element does not exist.
  12. set the bit (mask) of the element in the slot ( w) where the element is located to 1, indicating that the element is added
  13. Since the Add function can be accessed concurrently, bits[i] may be modified by other operations, so it is necessary to set the existence of the element in bits[i] by reloading (14) and by looping through it
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

func (f *filter) Add(h uint64) bool {
 bits := f.bits
 maxBits := uint64(len(bits)) * 64 //1
 bp := (*[8]byte)(unsafe.Pointer(&h))//2
 b := bp[:]
 isNew := false
 for i := 0; i < hashesCount; i++ {//3
  hi := xxhash.Sum64(b)//4
  h++ //5
  idx := hi % maxBits //6
  i := idx / 64 //7
  j := idx % 64 //8
  mask := uint64(1) << j //9
  w := atomic.LoadUint64(&bits[i])//10
  for (w & mask) == 0 {//11
   wNew := w | mask //12
   if atomic.CompareAndSwapUint64(&bits[i], w, wNew) {//13
    isNew = true//14
    break
   }
   w = atomic.LoadUint64(&bits[i])//14
  }
 }
 return isNew
}

Once you understand the Add function, Has is quite simple, it’s just a reduced version of the Add function, no need to set bits[i].

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

func (f *filter) Has(h uint64) bool {
 bits := f.bits
 maxBits := uint64(len(bits)) * 64
 bp := (*[8]byte)(unsafe.Pointer(&h))
 b := bp[:]
 for i := 0; i < hashesCount; i++ {
  hi := xxhash.Sum64(b)
  h++
  idx := hi % maxBits
  i := idx / 64
  j := idx % 64
  mask := uint64(1) << j
  w := atomic.LoadUint64(&bits[i])
  if (w & mask) == 0 {
   return false
  }
 }
 return true
}

Summary

Since VictoriaMetrics’ filter uses a Bloom filter, its speed limit is not precise, and is off by about 3% in source conditions. However, again, the use of Bloom filters reduces the memory required and the associated computational resources. In addition, VictoriaMetrics’ filters implement concurrent access. To support concurrent access, the filter uses atomic to store and load values and to change values.

In high-traffic scenarios where relatively accurate filtering of requests is required, consider using Bloom filters to reduce the resources required, provided that the filtered results can tolerate a certain level of miss-rate.