Java has a rich set of built-in container classes, and different containers are used to handle various business scenarios. Although Go has many similarities with Java in language design, it doesn’t support many container data structures natively, only map and slice. The standard library’s container package extends the container data structure to support three containers: Heap, LinkedList and Circular List.
Containers
Familiarity with C++ and Java should give you a clear understanding of containers, which are an integral part of modern programming practice and take many forms, generally described as objects with methods to manipulate the contents of the container.
- Built-in containers.
- map: Associated containers
- slice: dynamically expanding sequential container
- channels: queues
- container standard library (
pkg/container):- list: linkedlist container
- ring: circular List container
- heap: heap container, provides implementation of heap
slice, map and channel are the most common and built-in container data structures in Go, while all other containers are in the container package of the standard library. When using the container three containers, you don’t have to bother implementing algorithms related to data structures. Also, since all the input types supported by the containers provided by container are interface{}, you can handle any type of value as long as you implement the container’s interface.
container/list
The code for the linked list container list is an implementation of a Doubly Linked List. list maintains two constructs: Element and List.
|
|
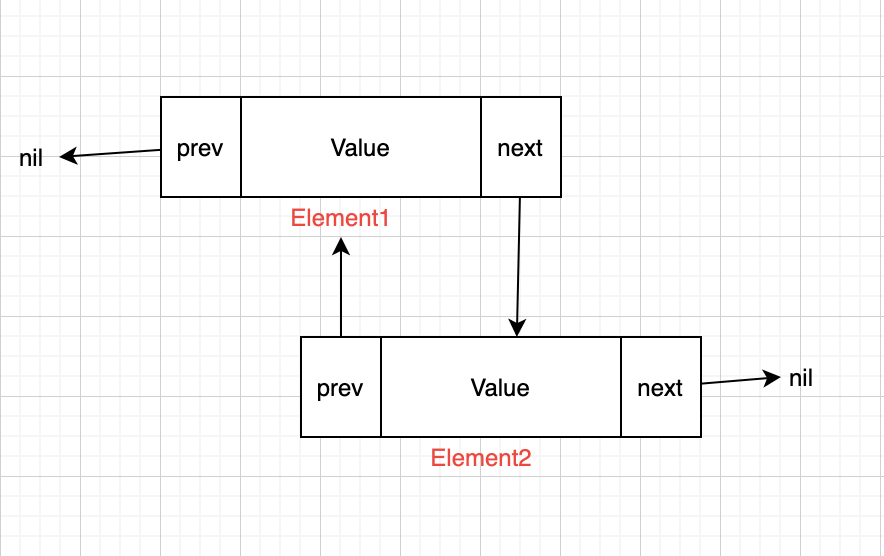
When a list is created with list.New(), an Element is initialized as a Root Pointer, which either points to the initial element of the list or is nil. In addition to the data field Value, each Element has prev and next that point to the direct predecessor and direct successor, respectively, to allow the user to move elements back and forth in the list.
The methods supported by the list container are as follows.
|
|
The following is a simple example of a list.
|
|
The output of this code is: 1234. After initializing the list, insert 4 at the end node and 1 at the head node; then insert 3 before the 4 and 2 after the 1, so the result is 1234.
The time complexity of list in inserting and deleting data is O(1); random lookup is less efficient, O(N) (slice random lookup has a time efficiency of O(1)).
A common application scenario for linkedlist containers is for doing LRU caching.
container/ring
The circular list container ring is a linkedlist with no head and tail nodes, and can be seen here as a simplified version of a list.
ring maintains a structure Ring.
|
|
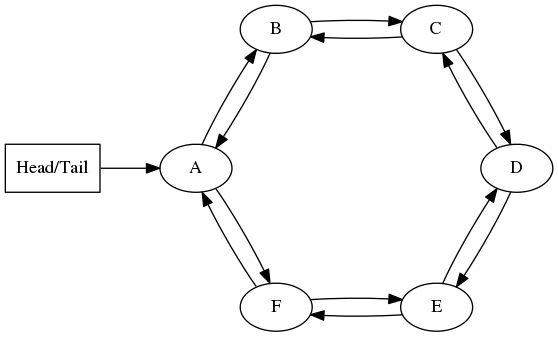
But unlike the list, the functions of the ring are not the same.
|
|
Here is a simple example of a ring.
|
|
The output of this code is 01234. After initializing the ring, the value of each element is assigned, and since the ring provides a Do method, the Print function is executed to print the result when the current element is traversed.
From the implementation of the ring, we know that the time complexity of the operation is O(N). Since ring nodes do not have head-to-tail distinction and FIFO characteristics, one application scenario where they can be used is ring buffers: providing mutually exclusive access to buffers without consuming resources.
container/heap
A heap is a complete binary tree implemented as an array. There are two types of heaps according to their characteristics: maximum heap and minimum heap, and the difference between them lies in the way the nodes are sorted.
- in the maximum heap, the value of the parent node is larger than the value of each child node, and the largest element of the heap is at the root node
- in the minimal heap, the value of the parent node is smaller than the value of each child node, and the smallest element of the heap is at the root node
Go’s heap container heap is implemented as a minimal heap, and the heap maintains an Interface.
|
|
Interface inlines sort.Interface, which implements three methods in addition to the out-of-heap method Push() and the in-heap method push().
|
|
As long as the data type of the Interface method is implemented, the minimum heap condition is met.
|
|
The heap.Init() function constructs a minimal heap (a slice sorted by precedence traversal), and the internal implementation of up() and down() adjusts the heap upward and downward, respectively.
Push(): When inserting an element into the heap, the element is inserted into the last node of the rightmost subtree, and thenup()is called to go up to ensure the minimum heap.Pop(): When pushing an element out of the heap, first swap the element with the last node of the right subtree, then pop the last node, and then calldown()on root to guarantee the minimum heap.
The methods supported by the heap container are as follows.
The following is an example of using a heap container to construct a priority queue pq.
|
|
The output of this code is 05:orange 04:pear 03:banana 02:apple. The first thing is to define a PriorityQueue array of structures as a queue, with a priority field identifying the priority, comparing the priority of two elements in the Less() method, and the queue update() for updating the priority of the elements. Then each time when executing heap.Pop(&pq). (*Item) operation, the element with high priority in the largest heap will be taken out of the heap.
The heap is initialized with a time complexity of O(N); the time complexity of entering the heap, exiting the heap, moving elements and rebuilding the minimum heap is O(logN).
Heap containers are more common in practice and are often used in production to implement priority queues and high performance timers.
Summary
In this article, we’ve sorted out Go’s container data structures, analyzed the three containers implemented by the container package in the standard library: list, ring and the more complex heap, and introduced their implementation, features and usage scenarios. Although slice and map are often used as containers in Go, if you find that these two data structures do not meet our needs in actual development, you can search under pkg/container to see if there are any available data structures.