Consistent Hash is often used to alleviate the problem of large cache failures caused by scaling up and down nodes in distributed caching systems. Consistent Hash is more of a load balancing strategy than a Hash algorithm.

GroupCache is an official golang distributed cache library that includes a simple implementation of Consistent Hash. The code is available at github.com/golang/groupcache/consistenthash. This article will provide insight into the principles of Consistency Hash based on GroupCache’s Consistency Hash implementation.

This paper will focus on the following points.

  1. the cache failure problem faced by traditional Hash-based load balancing during cluster expansion and contraction.
  2. the principle of Consistent Hash.
  3. how Golang’s open source library GroupCache implements Consistent Hash.

Caching problems due to cluster expansion and contraction

Let’s look at the traditional Hash-based load balancing and see what problems are encountered when the cluster is scaled up or down.

Suppose we have three cache servers, each used to cache a portion of the user’s information. The most common Hash load balancing practice is that for a given user, we can calculate the hash value of the user name or other unique information, and then divide the hash value by 3 to get the cache server corresponding to that user. This is shown in the figure below:

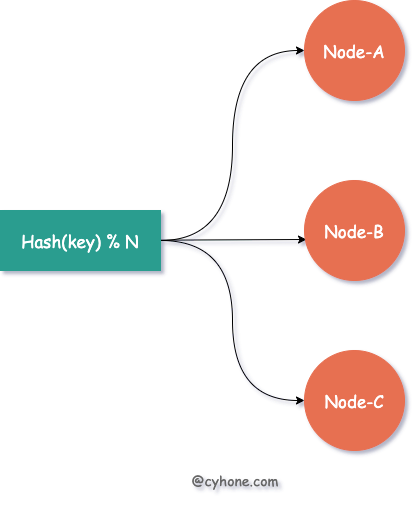
consistent-hash

When we need to expand or reduce the capacity of the cluster, adding or reducing some server nodes will cause large cache failures.

For example, if we need to expand a server from 3 to 4 cache servers, then the previous policy of hash(username) % 3 will be changed to hash(username) % 4. The whole load balancing policy is completely changed and there is a risk of hash failure for any user.

And once the cache fails en masse, all requests cannot hit the cache, and the client requests directly to the back-end service, the system is likely to crash.

Principle of Consistent Hash

In response to the above problem, if we use Consistent Hash as a load balancing strategy for the caching system, we can effectively alleviate the cache failure problem caused by cluster expansion and contraction.

In contrast to the direct hash modulo the target Server, Consistent Hash uses ordered Hash ring to select the target cache Server, as shown in the following figure.

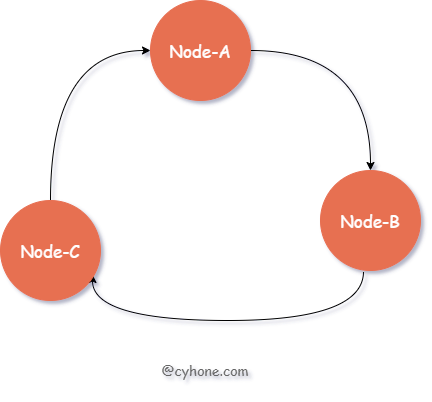
Consistent Hash

For this ordered Hash ring, each node in the ring corresponds to a cache server, and each node also contains an integer value. The nodes are ordered by that integer value from smallest to largest.

For a given user, we still first compute the hash value of the user name. Then, we search the Hash ring in order of value size, from smallest to largest, and find the first node that is greater than or equal to that hash value and use it as the target cache server.

For example, we have three nodes Node-A, Node-B, and Node-C in the hash ring with values of 3, 7, and 13, respectively, and assume that for a user, the hash value of his username is 9, and the first node in the ring greater than 9 is Node-C, then Node-C is chosen as the cache server for that user. Node-C

Cache Failure Mitigation

The above is the normal use of Consistent Hash. Next, let’s see how Consistent Hash copes with the expansion and contraction of the cluster.

When we expand the cluster and add a new node New-Node, assuming the value of the node is 11, then the new ordered Hash ring is as follows.

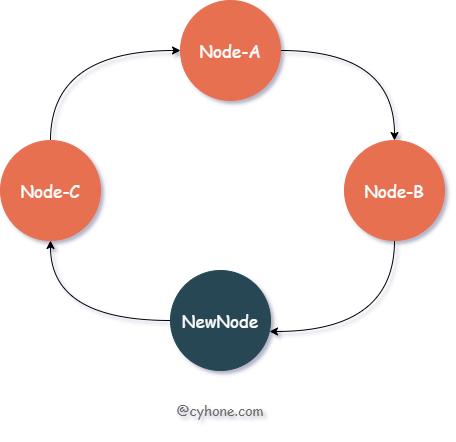
Cache Failure Mitigation

Let’s look at the cache invalidation scenario: in this case, only the data cache with hash values between Node-B and NewNode (i.e., (7, 11]) is invalidated. This data, which was assigned to node Node-C (value 13), now needs to be migrated to the new node NewNode.

The cached data that was assigned to nodes Node-A and Node-B will not be affected in any way. The data in the range between NewNode and Node-B (i.e., (11, 13]) is assigned to Node-C. After the new node appears, this data still belongs to Node-C and will not be affected in any way.

Consistent Hash makes use of the ordered Hash ring to cleverly mitigate the cache invalidation problem caused by cluster expansion and contraction. Note that we say “mitigate” here; cache invalidation cannot be completely avoided, but its impact can be minimized.

A small problem here is that since an ordered Hash ring requires each node in it to have hold an integer value, how is this integer value obtained? The general approach is that we can use the node’s unique information to calculate its Hash value, such as hash(ip:port).

Data Skewing and Virtual Nodes

The above describes the basic process of consistent hash, so it seems that consistent hash is indeed effective as a means to mitigate cache failures.

But let’s consider a limiting case. Suppose there are only two cache nodes in the whole cluster: Node-A and Node-B. Then Node-B will hold data with a Hash value in the range (Node-A, Node-B]. And Node-A will take two parts of the data: hash < Node-A and hash > Node-B.

From this range of values, we can easily see that the value space of Node-A is actually much larger than that of Node-B. When the amount of data is large, Node-A will also carry much more data than Node-B. In fact, when there are too few nodes, it is easy to allocate far more data to one node than to others. This phenomenon we often call `Data Skew'.

For such problems, we can introduce the concept of virtual nodes, or replica nodes. Each real cache Server corresponds to multiple virtual nodes on the Hash ring. This is shown in the following figure.

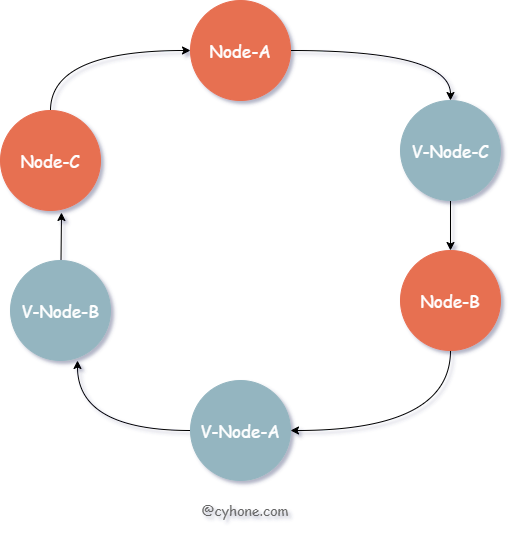
Data Skewing and Virtual Nodes

For the above diagram, we still have only three cache servers, but each server has a copy, e.g. V-Node-A and Node-A both correspond to the same cache server.

Consistent Hash Implementation of #GroupCache

GroupCache provides a simple implementation of consistent hash. The code is available at github.com/golang/groupcache/consistenthash.

Let’s look at how it is used.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import (
    "fmt"
    "github.com/golang/groupcache/consistenthash"
)

func main() {
    // 构造一个 consistenthash 对象，每个节点在 Hash 环上都一共有三个虚拟节点。
    hash := consistenthash.New(3, nil)

    // 添加节点
    hash.Add(
        "127.0.0.1:8080",
        "127.0.0.1:8081",
        "127.0.0.1:8082",
    )

    // 根据 key 获取其对应的节点
    node := hash.Get("cyhone.com")

    fmt.Println(node)
}

consistenthash provides three functions for external use.

  1. New(replicas int, fn Hash): construct a consistenthash object, replicas represents the number of virtual nodes for each node, for example replicas equals 3, which means that each node corresponds to three virtual nodes on the Hash ring. fn represents a custom hash function, passing nil will use the default hash function.
  2. the Add function: adds nodes to the Hash ring; 3. the Get function: adds nodes to the Hash ring.
  3. Get function: pass in a key and get the node it is assigned to.

Add function

The Add function is used to add nodes to the Hash ring. Its source code is as follows.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func (m *Map) Add(keys ...string) {
    for _, key := range keys {
        for i := 0; i < m.replicas; i++ {
            hash := int(m.hash([]byte(strconv.Itoa(i) + key)))
            m.keys = append(m.keys, hash)
            m.hashMap[hash] = key
        }
    }

    // 排序，这个动作非常重要，因为只有这样，才能构造一个有序的 Hash 环
    sort.Ints(m.keys)
}

There are two important properties involved in the Add function. 1:

  1. keys: type []int. This is actually the ordered Hash ring we mentioned above, represented here as an array. Each item in the array represents a virtual node and its value.
  2. hashMap: type map[int]string . This is the mapping of virtual nodes to real nodes passed by the user. map’s key is the element of the keys property.

In this function, there is an operation to generate virtual nodes. For example, if the user passes ["Node-A", "Node-B"] with replicas equal to 2, then Node-A will correspond to two virtual nodes in the Hash ring: 0Node-A, 1Node-A, and the values corresponding to these two nodes will be obtained by directly computing hash on them.

Note that the function will sort the keys at the end of each Add. So it is better to add all the nodes at once to avoid multiple sorting.

Get function

Next, we analyze the use of the Get function, which is used to assign the corresponding node to the specified key. The source code is as follows.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

func (m *Map) Get(key string) string {
    if m.IsEmpty() {
        return ""
    }

    hash := int(m.hash([]byte(key)))

    // Binary search for appropriate replica.
    // 二分查找
    idx := sort.Search(len(m.keys), func(i int) bool { return m.keys[i] >= hash })

    // Means we have cycled back to the first replica.
    // 如果没有找到，则使用首元素
    if idx == len(m.keys) {
        idx = 0
    }

    return m.hashMap[m.keys[idx]]
}

First calculate the hash value of the key passed by the user, and then use sort.Search to dichotomize in keys to get the smallest value in the array that satisfies the situation. Since keys is an ordered array, using dichotomous search can speed up the query.

If not found, then use the first element, this is the basic operation of the ring array. Finally, use hashMap[keys[idx]] to get the real node from the virtual node.

The above is the implementation of Groupcache for Consistent Hash. This implementation is simple and effective, and can help us understand the principle of Consistent Hash quickly.