1. Introduction

OverScroller in Android is responsible for calculating the real-time sliding position for ListView, RecyclerView, ScrollView and other scrolling controls, and these position algorithms directly affect the experience of each scroll.

As we all know, Android’s animation experience is ~far~ inferior to iOS, and even now that Android generally supports 120Hz high swipe, the experience is not very comfortable. The reason for this is no longer hardware performance limitations, but the design of many of these animations is inherently problematic. Apple released Designing Fluid Interfaces a long time ago to create a silky smooth user experience, on the contrary, Android, for a daily use of the most used swipe tool class Odel The most used sliding tool class on Android, OverScroller, has seen very few improvements in recent years, almost none, which is really something I want to spit out.

This series is divided into two articles, the first one is about the usage and principle of OverScroller, the core tool class for Android scrolling, and the second one will explore how to improve it, hoping that each exploration will bring improvement to the user experience.

2. Introduction to use

Before we use it, let’s see what OverScroller can do.

  • startScroll: Scrolls a specified distance from a specified position and then stops, the scrolling effect is related to the set scroll distance, scroll time, interpolator, not related to the off-hand speed. Generally used to control the View scrolling to the specified position.
  • fling: slide a position from the specified position and then stop, the scrolling effect is only related to the off-hand speed and sliding boundary, not set the scrolling distance, scrolling time and interpolator. Generally used to continue to let the View slide for a while after touching the raised hand.
  • springBack: spring back from the specified position to the specified position, generally used to achieve the spring back effect after dragging, can not specify the spring back time and interpolator.
startScroll fling springBack
startScroll fling springBack

It is also simple to use in code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// 1. 启动一个滚动
mOverScroller.startScroll(0, 1600, 0, -1000, 1000);
// 2. 启动定时刷新任务
post(new Runnable() {
    
    public void run() {
        // 3. 计算当前最新位置信息
        if (mOverScroller.computeScrollOffset()) {
            // 4. 根据最新位置更新 View 状态
            Log.d("OverScroller", "x=" + mOverScroller.getCurrX() + ", y=" + mOverScroller.getCurrY());
            invalidate();
            // 5. 判断滚动是否停止，没有停止的话启动下一轮刷新任务
            if (!mOverScroller.isFinished()) {
                postDelayed(this, 16);
            }
        }
    }
});

The above is the minimal logic to start a constantly scrolling and refreshing View (of course a more engineering approach could also put the Runnable logic in View#computeScroll and trigger it via invalidate). fling and springBack are started in the same way, so we won’t go into details here.

3. Deep inside the OverScroller

As you can see in the above code, after starting a scrolling task, the position is computed by calling computeScrollOffset again and again, so let’s look at the code implementation

3.1 startScroll

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public class OverScroller {

    public void startScroll(int startX, int startY, int dx, int dy, int duration) {
        // 标记当前模式为 SCROLL_MODE
        mMode = SCROLL_MODE;
        // mScrollerX 和 mScrollerY 均是 SplineOverScroller 实例
        // OverScroller 把参数分别传给 mScrollerX 和 mScrollerY，在里面做真正的计算
        mScrollerX.startScroll(startX, dx, duration);
        mScrollerY.startScroll(startY, dy, duration);
    }

    static class SplineOverScroller {
        void startScroll(int start, int distance, int duration) {
            mFinished = false;
            // 标记起始点和结束点
            mCurrentPosition = mStart = start;
            mFinal = start + distance;

            // 标记起始时间和动画时长
            mStartTime = AnimationUtils.currentAnimationTimeMillis();
            mDuration = duration;

            // Unused
            mDeceleration = 0.0f;
            mVelocity = 0;
        }
    }
}

The logic of startScroll is very simple, it just marks the start position, end position, start time and animation duration according to the parameters, it doesn’t involve the position calculation (because the position calculation is placed in the computeScrollOffset).

And look at the logic of computeScrollOffset called at regular intervals.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

public class OverScroller {

    public OverScroller(Context context, Interpolator interpolator, boolean flywheel) {
        // 初始化插值器
        if (interpolator == null) {
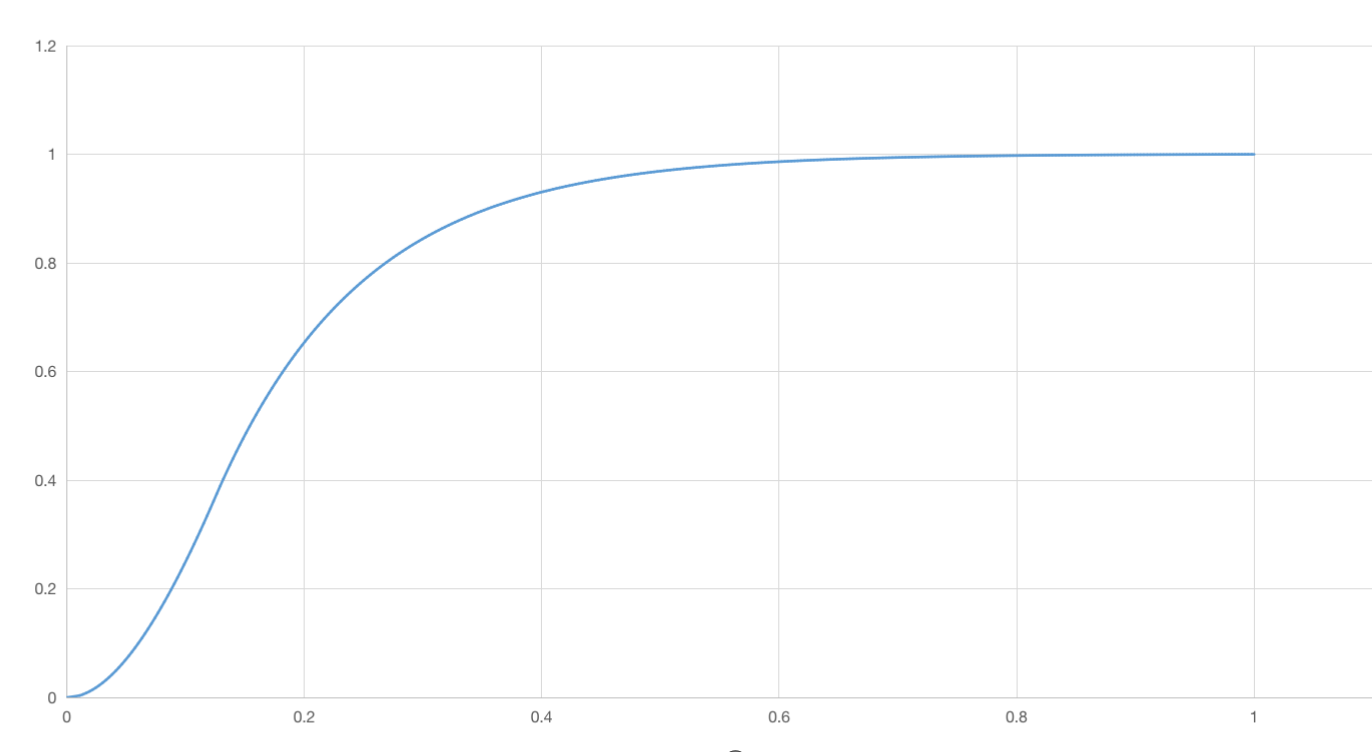
            mInterpolator = new Scroller.ViscousFluidInterpolator();
        } else {
            mInterpolator = interpolator;
        }
        ...
    }

    public boolean computeScrollOffset() {
        if (isFinished()) {
            return false;
        }
        switch (mMode) {
            case SCROLL_MODE:
                long time = AnimationUtils.currentAnimationTimeMillis();
                // 计算已过去的时间
                final long elapsedTime = time - mScrollerX.mStartTime;

                final int duration = mScrollerX.mDuration;
                if (elapsedTime < duration) {
                    // 用插值器对时间比做一个变换
                    final float q = mInterpolator.getInterpolation(elapsedTime / (float) duration);
                    mScrollerX.updateScroll(q);
                    mScrollerY.updateScroll(q);
                } else {
                    abortAnimation();
                }
                break;
            break;
        }
        return true;
    }

    static class SplineOverScroller {

        void updateScroll(float q) {
            // 根据比值计算最新位置
            mCurrentPosition = mStart + Math.round(q * (mFinal - mStart));
        }
    }
}

Logic is also very simple, there is really not much to say …… is to map the interpolator curve to the displacement curve, the duration if not specified, the default is 250ms, the interpolator needs to be passed through the construction method, if not specified, the system will specify a ViscousFluidInterpolator by default, the following is the curve of this interpolator, you can see is a first slow then fast then slow animation.

ViscousFluidInterpolator

3.2 fling & springBack

Why do fling and springBack need to be mentioned together? Because the animation of fling is more complex, and springBack is sort of a sub-state of fling, consider the following case.

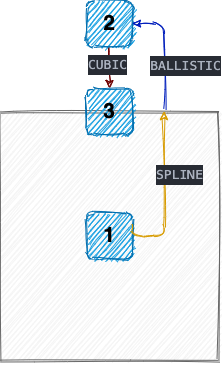
sobyte

sobyte

We see that when fling is executed at a relatively large speed, it is very easy to hit the boundary, and fling will execute the boundary crossing and bounce back according to the preset boundary value, which can decompose the whole animation process into three stages.

  • SPLINE: that is, the normal sliding stage
  • BALLISTIC: The deceleration phase of boundary crossing
  • CUBIC: the rebound phase

The animation executed after springBack is actually the CUBIC phase of fling, so we simply put it together.

The naming is actually quite interesting, these three are sample curve, ballistic curve, and three times curve, from the naming, we can roughly infer that the “time-position” curves used in the three phases are different.

Of course, a lot of Android controls will cancel the boundary rebound effect when flinging, and display an EdgeEffect instead. In other words, after executing the SPLINE stage animation, you can’t see BALLISTIC and CUBIC, you can only see an edge glow effect, and when the list reaches the top/bottom, it often stops there at once~.

3.2.1 SPLINE

First, let’s look at the entry function that starts fling.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

public class OverScroller {

    public void fling(int startX, int startY, int velocityX, int velocityY,
            int minX, int maxX, int minY, int maxY, int overX, int overY) {
        // 标记滚动模式，主要和 startScroll 进行区分
        mMode = FLING_MODE;
        mScrollerX.fling(startX, velocityX, minX, maxX, overX);
        mScrollerY.fling(startY, velocityY, minY, maxY, overY);
    }

    static class SplineOverScroller {

        void fling(int start, int velocity, int min, int max, int over) {
            mOver = over;
            mFinished = false;
            mCurrVelocity = mVelocity = velocity;
            mDuration = mSplineDuration = 0;
            mStartTime = AnimationUtils.currentAnimationTimeMillis();
            mCurrentPosition = mStart = start;

            mState = SPLINE;
            double totalDistance = 0.0;

            if (velocity != 0) {
                // 根据速度计算滑动时长
                mDuration = mSplineDuration = getSplineFlingDuration(velocity);
                // 根据速度计算滑动距离
                totalDistance = getSplineFlingDistance(velocity);
            }

            mSplineDistance = (int) (totalDistance * Math.signum(velocity));
            mFinal = start + mSplineDistance;

            if (mFinal < min) {
                // 如果计算出的滑动距离超过 min 边界，则重新计算到达 min 边界时的滑动时长
                adjustDuration(mStart, mFinal, min);
                mFinal = min;
            }

            if (mFinal > max) {
                // 如果计算出的滑动距离超过 max 边界，则重新计算到达 max 边界时的滑动时长
                adjustDuration(mStart, mFinal, max);
                mFinal = max;
            }
        }

        private double getSplineDeceleration(int velocity) {
            return Math.log(INFLEXION * Math.abs(velocity) / (mFlingFriction * mPhysicalCoeff));
        }

        /**
         * 计算滑动距离
         */
        private double getSplineFlingDistance(int velocity) {
            final double l = getSplineDeceleration(velocity);
            final double decelMinusOne = DECELERATION_RATE - 1.0;
            return mFlingFriction * mPhysicalCoeff * Math.exp(DECELERATION_RATE / decelMinusOne * l);
        }

        /**
         * 计算滑动时长
         */
        private int getSplineFlingDuration(int velocity) {
            final double l = getSplineDeceleration(velocity);
            final double decelMinusOne = DECELERATION_RATE - 1.0;
            return (int) (1000.0 * Math.exp(l / decelMinusOne));
        }
    }
}

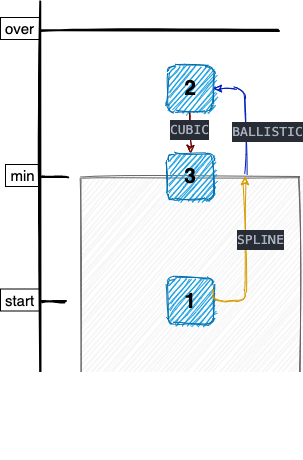
sobyte

Before looking at the code, let’s take a look at the above diagram, which illustrates the meaning of start, min, max, over, etc. Here is a brief explanation

  • The final stopping position after flinging must be between min and max
  • The BALLISTIC crossing phase cannot exceed the over position, i.e., over is the maximum crossing distance.
  • start can be located outside the [min, max] interval, if it is outside the interval, a decision will be made based on the direction and size of the velocity, there will be three cases as follows.
    • velocity pointing out of bounds: execute BALLISTIC to cross the bounds first and then execute CUBIC to bounce back to the bounds
    • Velocity pointing inside the boundary: If the velocity is enough to cross the boundary, the normal process will be executed, and SPLINE will be executed first.
    • Speed pointing inside the boundary: if the speed is not enough to cross the boundary, execute CUBIC directly back to the boundary

The main functions of the fling function are

  • Calculate the duration and distance of the slide based on the starting speed.
  • If the final point is outside the [min, max] interval, recalculate the time to reach the boundary.
  • Mark the current state as SPLINE state

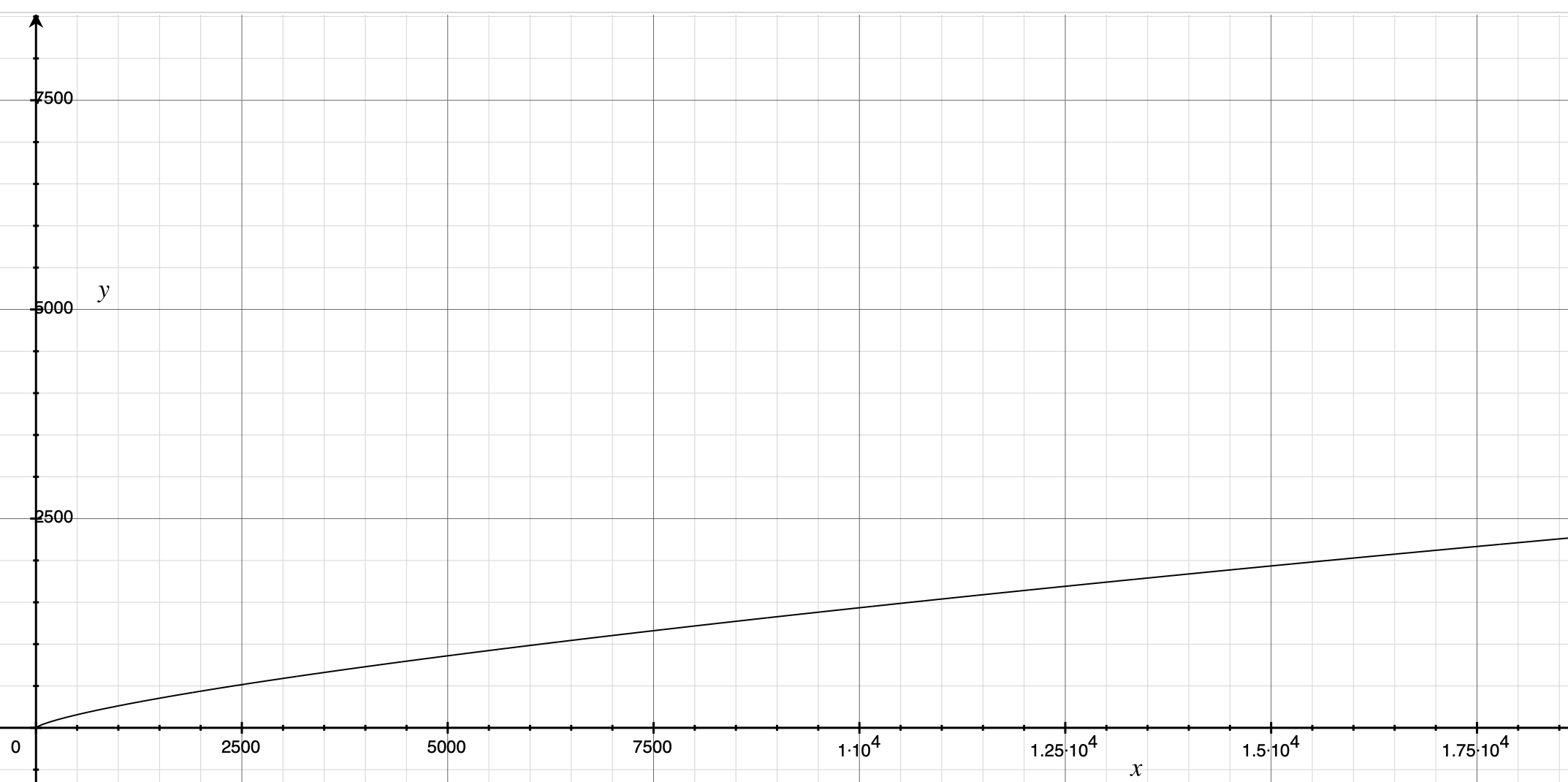
The equations for the sliding distance and duration can be calculated by considering mPhysicalCoeff as a constant as well, listing the time-velocity equation and the image.

$$y=1000\cdot \exp \left( \frac{\ln \left( \frac{0.35x}{2140.47} \right)}{1.358} \right)$$

sobyte

Look again at the distance-velocity equation.

$$y=2140.47\cdot \exp \left( 1.74\cdot \ln \left( \frac{0.35\cdot x}{2140.47} \right) \right)$$

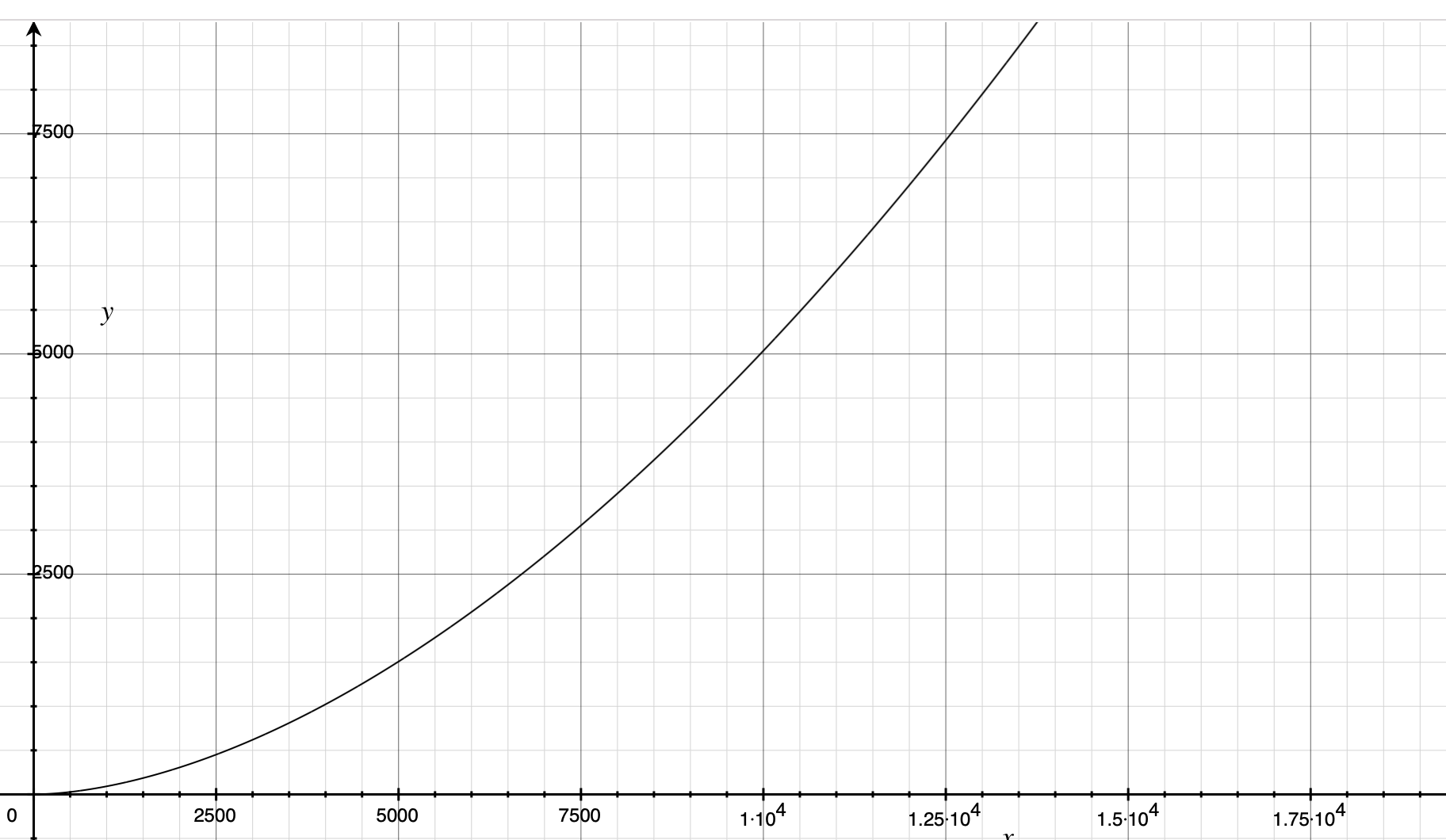
sobyte

As you can see, both distance and duration increase with speed, but the growth rate of duration converges at a later stage to ensure that the animation duration is not too long.

Another point to note is that the ratio of $ \frac{Distance} {Duration} $ is a linear function, that is, the larger the initial velocity, the larger the average velocity, and the two are growing linearly.

$$y=\frac{2140.47\cdot \exp \left( 1.74\cdot \ln \left( \frac{0.35\cdot x}{2140.47} \right) \right)}{1000\cdot \exp \left( \frac{\ln \left( \frac{0.35x}{2140.47} \right)}{1.358} \right)}$$

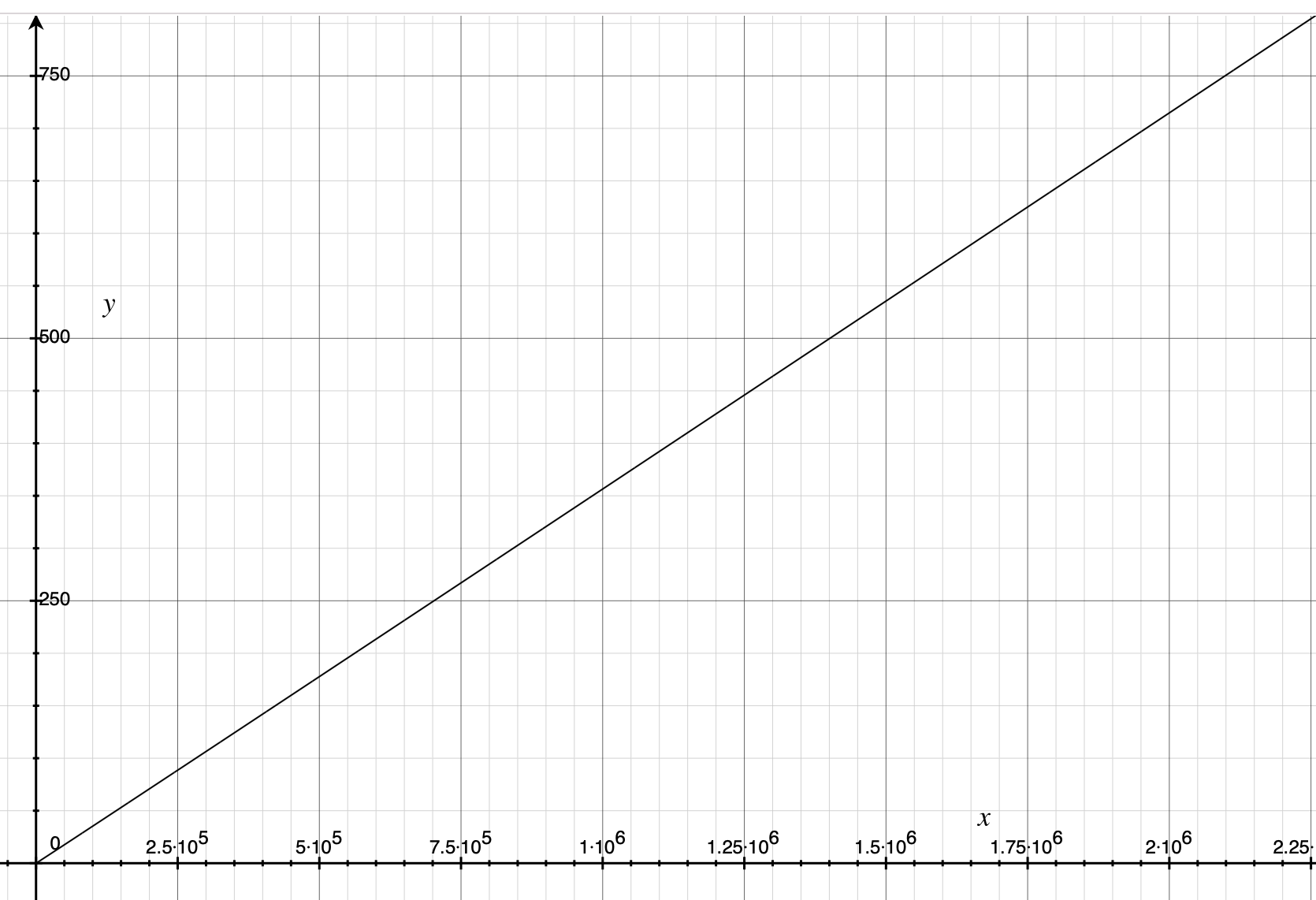
sobyte

But to be honest, at present I temporarily did not understand the physical meaning of these two formulas, there is an understanding of the big brother please tell ~ Is the use of the logarithmic function of convergence to determine the length of the formula, and then set the average speed of linear growth, after deducing the distance formula?

At present, only the total distance and length of the slide are determined, so how is the intermediate process to update the position.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117

public class OverScroller {

    public boolean computeScrollOffset() {
        if (isFinished()) {
            return false;
        }

        switch (mMode) {
            case FLING_MODE:
                ...
                if (!mScrollerY.mFinished) {
                    // 更新当前阶段的速度和位置
                    if (!mScrollerY.update()) {
                        // 判断是否需要进入下一动画阶段
                        if (!mScrollerY.continueWhenFinished()) {
                            mScrollerY.finish();
                        }
                    }
                }
                break;
        }
        return true;
    }

    static class SplineOverScroller {

        boolean update() {
            final long time = AnimationUtils.currentAnimationTimeMillis();
            final long currentTime = time - mStartTime;

            if (currentTime == 0) {
                return mDuration > 0;
            }
            // 根据动画时长判断当前阶段的动画是否应该结束
            if (currentTime > mDuration) {
                return false;
            }

            double distance = 0.0;
            switch (mState) {
                case SPLINE: {
                    // 把当前时间映射到 100 个采样点的曲线之中
                    final float t = (float) currentTime / mSplineDuration;
                    final int index = (int) (NB_SAMPLES * t);
                    float distanceCoef = 1.f;
                    float velocityCoef = 0.f;
                    if (index < NB_SAMPLES) {
                        final float t_inf = (float) index / NB_SAMPLES;
                        final float t_sup = (float) (index + 1) / NB_SAMPLES;
                        final float d_inf = SPLINE_POSITION[index];
                        final float d_sup = SPLINE_POSITION[index + 1];
                        // 根据映射时间计算样条曲线的当前的斜率，即速度
                        velocityCoef = (d_sup - d_inf) / (t_sup - t_inf);
                        // 根据映射时间计算样条曲线的高度，即距离
                        distanceCoef = d_inf + (t - t_inf) * velocityCoef;
                    }
                    // 把样条距离映射回真正的距离
                    distance = distanceCoef * mSplineDistance;
                    // 把样条速递易映射回真正的速度
                    mCurrVelocity = velocityCoef * mSplineDistance / mSplineDuration * 1000.0f;
                    break;
                }

                case BALLISTIC: {
                    // 根据匀减速运动公式计算位置和速度
                    final float t = currentTime / 1000.0f;
                    mCurrVelocity = mVelocity + mDeceleration * t;
                    distance = mVelocity * t + mDeceleration * t * t / 2.0f;
                    break;
                }

                case CUBIC: {
                    // 根据一个自定义的三次曲线计算位置和速度
                    final float t = (float) (currentTime) / mDuration;
                    final float t2 = t * t;
                    final float sign = Math.signum(mVelocity);
                    distance = sign * mOver * (3.0f * t2 - 2.0f * t * t2);
                    mCurrVelocity = sign * mOver * 6.0f * (- t + t2);
                    break;
                }
            }

            mCurrentPosition = mStart + (int) Math.round(distance);

            return true;
        }

        boolean continueWhenFinished() {
            switch (mState) {
                case SPLINE:
                    if (mDuration < mSplineDuration) {
                        // 如果时长小于 mSplineDuration ，说明 mDuration 被重新计算过，即上面说到的到达边界的时间。那么我们需要进入越界状态
                        mCurrentPosition = mStart = mFinal;
                        mVelocity = (int) mCurrVelocity;
                        mDeceleration = getDeceleration(mVelocity);
                        mStartTime += mDuration;
                        onEdgeReached();
                    } else {
                        // SPLINE 停止时未到达边界，结束动画
                        return false;
                    }
                    break;
                case BALLISTIC:
                    // 越界状态结束，进入回弹阶段
                    mStartTime += mDuration;
                    startSpringback(mFinal, mStart, 0);
                    break;
                case CUBIC:
                    // 回弹阶段结束，结束动画
                    return false;
            }

            update();
            return true;
        }
    }
}

The position and velocity of the SPLINE stage are determined entirely by the preset SPLINE_POSITION spline curve, which is an array of size 101 that stores the coordinate values of a curve sampled 100 times on average, initialized as follows.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

private static final int NB_SAMPLES = 100;
private static final float[] SPLINE_POSITION = new float[NB_SAMPLES + 1];
private static final float[] SPLINE_TIME = new float[NB_SAMPLES + 1];

static {
    float x_min = 0.0f;
    float y_min = 0.0f;
    for (int i = 0; i < NB_SAMPLES; i++) {
        final float alpha = (float) i / NB_SAMPLES;

        float x_max = 1.0f;
        float x, tx, coef;
        while (true) {
            x = x_min + (x_max - x_min) / 2.0f;
            coef = 3.0f * x * (1.0f - x);
            tx = coef * ((1.0f - x) * P1 + x * P2) + x * x * x;
            if (Math.abs(tx - alpha) < 1E-5) break;
            if (tx > alpha) x_max = x;
            else x_min = x;
        }
        SPLINE_POSITION[i] = coef * ((1.0f - x) * START_TENSION + x) + x * x * x;
    }
    SPLINE_POSITION[NB_SAMPLES] = SPLINE_TIME[NB_SAMPLES] = 1.0f;
}

It’s hard to imagine what it looks like by looking at the code, so let’s look at the image directly.

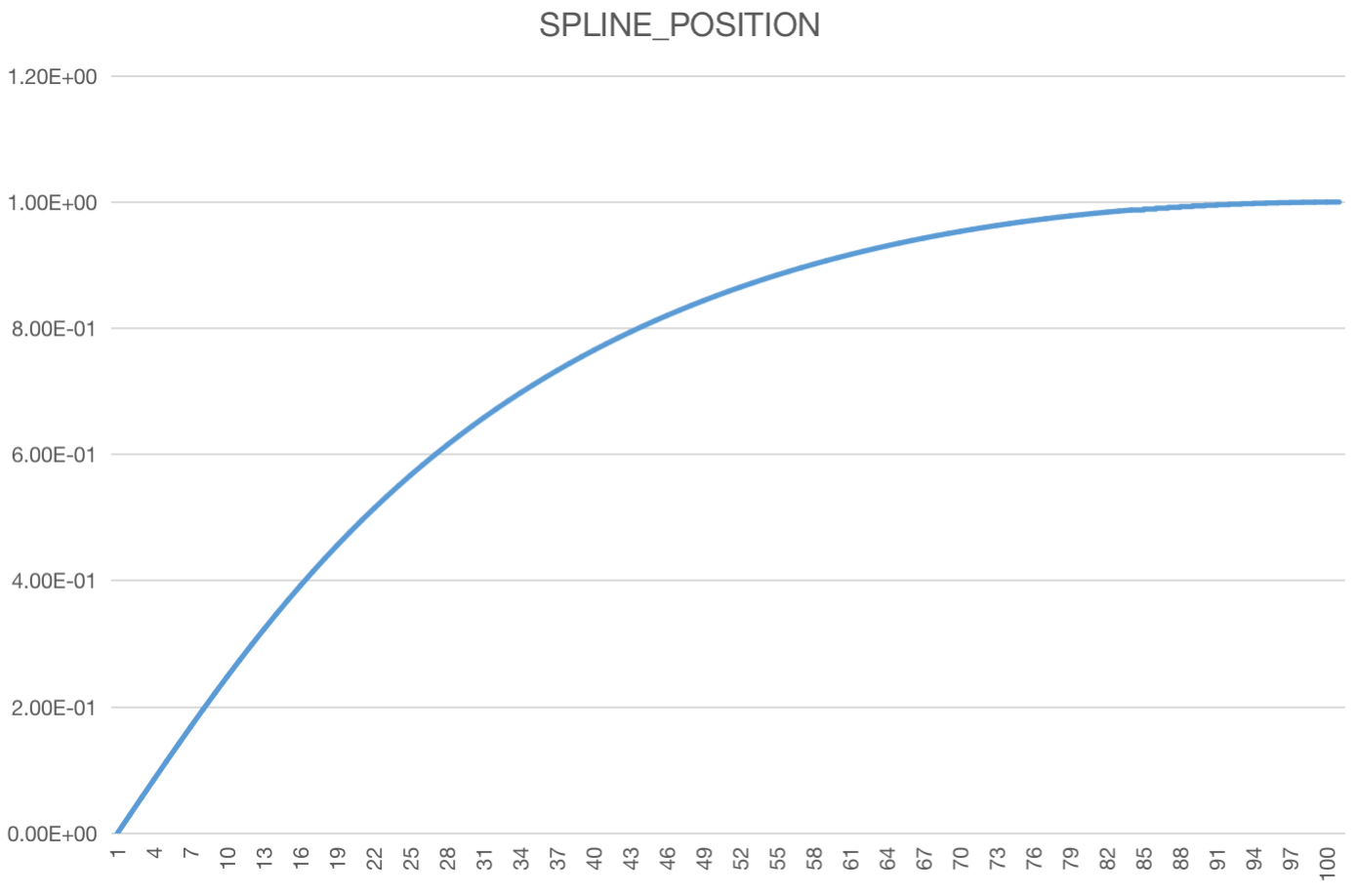
sobyte

That is, SPLINE and startScroll are much like each other in that the position curve is determined by a preset curve that maps the preset curve to the true distance, except that instead of using an interpolator curve, SPLINE uses a slow-stop spline curve.

3.2.2 BALLISTIC

At the end of the SPLINE phase, the next phase is continued by continueWhenFinished: the boundary crossing phase (provided that the boundary has been reached). The principle of the boundary crossing phase is relatively simple, it is a period of uniform deceleration (until the velocity drops to 0), and the default acceleration a is -2000.0f. The initialization logic to enter the BALLISTIC phase is in onEdgeReached.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

private void onEdgeReached() {
    final float velocitySquared = (float) mVelocity * mVelocity;
    // 计算速度降为 0 时，运动的距离
    float distance = velocitySquared / (2.0f * Math.abs(mDeceleration));
    final float sign = Math.signum(mVelocity);

    if (distance > mOver) {
            // 如果距离大于最大距离 over，则重新计算加速度，使运动距离恰好为 over
            mDeceleration = - sign * velocitySquared / (2.0f * mOver);
            distance = mOver;
    }

    mOver = (int) distance;
    // 标记动画阶段
    mState = BALLISTIC;
    mFinal = mStart + (int) (mVelocity > 0 ? distance : -distance);
    // 根据初速度和加速度计算总时长
    mDuration = - (int) (1000.0f * mVelocity / mDeceleration);
}

Speed.

$$v_t=v_0+at$$

Distance.

$$s_t=v_0t + \frac{at^2} {2}$$

There is a small complaint here, the acceleration is fixed at 2000, which is too small, that is, if the crossing speed is 10000, then it takes 5s for the speed to drop to 0. A 5s animation you all know how long it means, right?

3.2.3 CUBIC

As we know from the previous section, the speed is reduced to 0 at the end of the BALLISTIC phase, and we finally come to the last section, where startSpringback is called from continueWhenFinished as the initialization of CUBIC.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

private void startSpringback(int start, int end, int velocity) {
    mFinished = false;
    // 标记动画阶段
    mState = CUBIC;
    mCurrentPosition = mStart = start;
    mFinal = end;
    // CUBIC 阶段运动总距离
    final int delta = start - end;
    mDeceleration = getDeceleration(delta);
    mVelocity = -delta; // only sign is used
    mOver = Math.abs(delta);
    // 计算此阶段的动画时长
    mDuration = (int) (1000.0 * Math.sqrt(-2.0 * delta / mDeceleration));
}

The time calculation still uses the logic of uniformly accelerated linear motion, imagining a section with initial velocity 0, acceleration a, and distance delta.

$$delta=\frac{(v_0 + v_t)} {2} t$$

Then.

$$ v_0=0，v_t=at $，那么 $ delta=\frac{at^2} {2} $，$ t=\sqrt{ \frac{2*delta} {a}}$$

In the update method, the core logic of updating CUBIC is.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

case CUBIC: {
    // 根据一个自定义的三次曲线计算位置和速度
    final float t = (float) (currentTime) / mDuration;
    final float t2 = t * t;
    final float sign = Math.signum(mVelocity);
    // 计算运动位置
    distance = sign * mOver * (3.0f * t2 - 2.0f * t * t2);
    // 计算速度，对距离公式求导即可
    mCurrVelocity = sign * mOver * 6.0f * (- t + t2);
    break;
}

The core logic is this 3.0f * t2 - 2.0f * t * t2 , which is actually a more commonly used cubic curve.

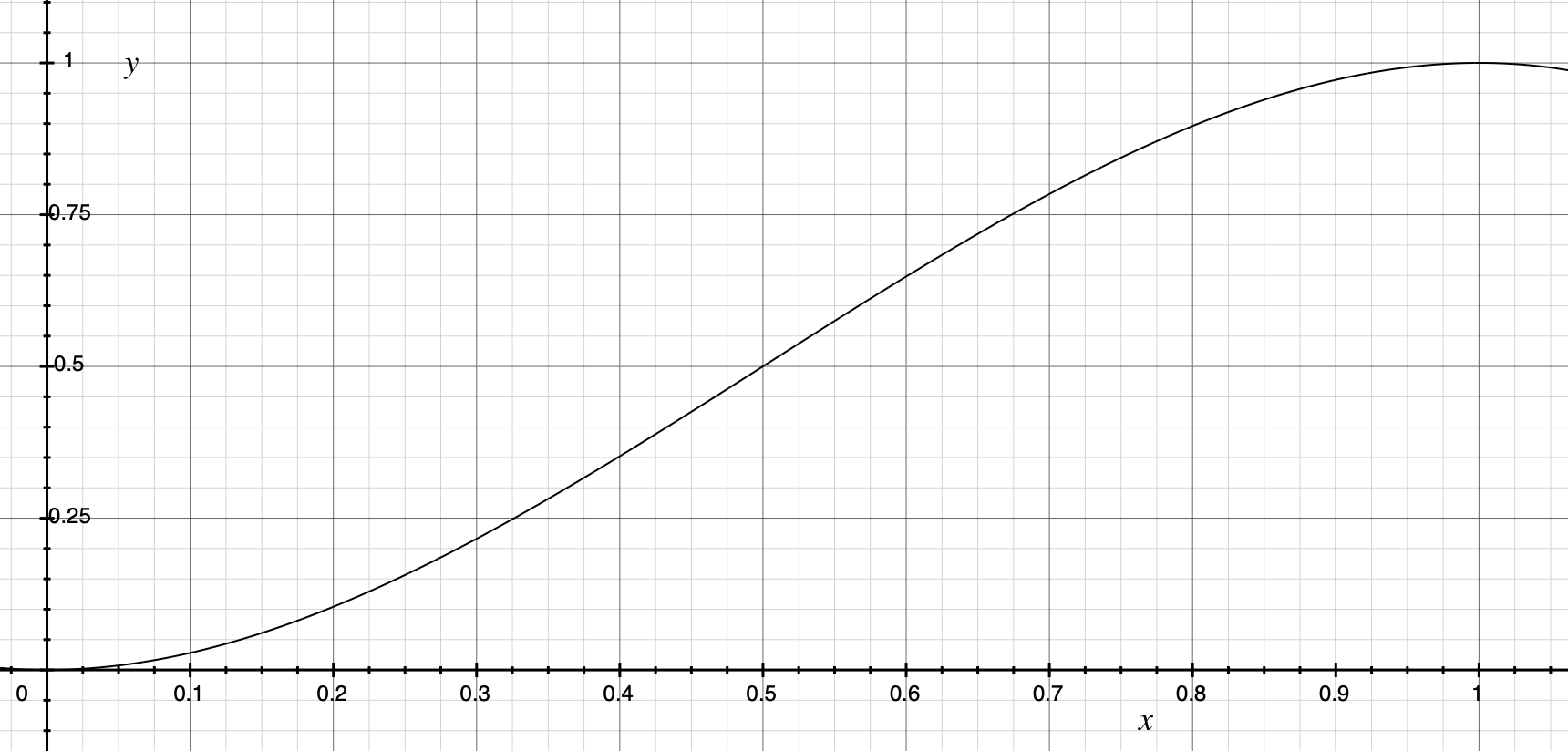
sobyte

In the interval [0, 1], it is a slow-in and slow-out curve. At this point, the motion law of CUBIC is also clear, which maps the time to the interval [0, 1] at a fixed time, and then maps the y-coordinate to the actual position.

4. Summary

So far, we have finally looked at the curves of startScroll and fling stages, as for springBack and some other cases, they are more or less the same, so we won’t go into details.

Many times OverScroller just uses a fixed curve to map the real curve, such as startScroll, SPLINE and CUBIC, so if you want to change the effect, is it possible to modify the shape of the curve? But can a curve really perform better at different speeds? Maybe we have to have a lot of practice and experimentation to make a section to make the user comfortable sliding.