In the program development, we often encounter a tree structure to represent the relationship between certain data, such as the organizational structure of the enterprise, the classification of goods, operation columns, etc., the current relational database is to store data in the form of two-dimensional table records, and the tree structure of the data must be stored in the two-dimensional table Schema design. Recently, we have been interested in this area, and we are dedicated to sorting out the following common tree structure data.

Adjacency List Pattern Adjacency List

The simplest method is: Adjacency List (Adjacency List pattern). It simply describes the parent node of a node based on the inheritance relationship between nodes, thus creating a two-bit relationship table. The table structure is usually designed as {Node_id,Parent_id}, as follows.

Approximate code for using the join table.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

<?php
// $parent is the parent of the children we want to see
// $level is increased when we go deeper into the tree,
//        used to display a nice indented tree

function display_children($parent, $level) 
{
   // 获得一个 父节点 $parent 的所有子节点
   $result = mysql_query('SELECT name FROM tree WHERE parent="'.$parent.'";');

   // 显示每个子节点
   while ($row = mysql_fetch_array($result)) 
   {
       // 缩进显示节点名称
       echo str_repeat('  ',$level).$row['name']."\n";

       //再次调用这个函数显示子节点的子节点
      
       display_children($row['name'], $level+1);
   }
}
?>

Using this function for the root node of the entire structure (Food) will print out the entire multilevel tree structure. Since Food is the root node its parent is empty, so call it like this: display_children(",0). will display the entire tree. If you want to display only a part of the whole structure, say the fruit part, call it like this: display_children(‘Fruit’,0);

Using almost the same method we can know the path from the root node to any node. For example, Cherry’s path is “Food >; Fruit >; Red”. To get such a path we need to start from the deepest level “Cherry”, query its parent node “Red” and add it to the path, then we query Red’s parent node and add it to the path as well. And so on up to the highest level “Food”

Here is the code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

<?php
// $node 是那个最深的节点
function get_path($node) 
{
   // 查询这个节点的父节点
   $result = mysql_query('SELECT parent FROM tree '.
                          'WHERE name="'.$node.'";');
   $row = mysql_fetch_array($result);

   // 用一个数组保存路径
   $path = array();

   // 如果不是根节点则继续向上查询
   // (根节点没有父节点)
   if ($row['parent']!='') 
   {
       // the last part of the path to $node, is the name
       // of the parent of $node
       $path[] = $row['parent'];

       // we should add the path to the parent of this node
       // to the path
       $path = array_merge(get_path($row['parent']), $path);
   }

   // return the path
   return $path;
}
?>

If you use this function for “Cherry”: print_r(get_path(‘Cherry’)), you will get an array like this

1
2
3
4
5
6

Array  
(  
  [0] =>; Food  
  [1] =>; Fruit  
  [2] =>; Red  
)

The advantages of this scheme are obvious: the structure is simple and easy to understand, and since the relationship between them is maintained by a single parent_id, it is very easy to add, delete, and change only the records directly related to it. The disadvantage of course is also very prominent: since the inheritance relationship between nodes is directly recorded, any CRUD operation on the Tree will be inefficient, mainly due to the frequent “recursive” operations, where the recursive process constantly accesses the database and each database IO has a time overhead. For example, if you want to return all the fruits, that is, all the children nodes of the fruits, a seemingly simple operation, you need to use a bunch of recursion. Of course, this scheme is not useless, when the tree level is relatively small is very practical, based on the neighbor list pattern can also be expanded is a flat table, the difference is the level of the node and the order of the current node is also put into the table, more suitable for similar comments and other scenarios, the specific table structure similar to this, here will not elaborate in depth.

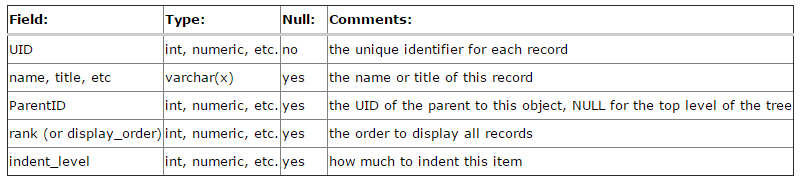
Path Enumeration

The materialized path is actually easier to understand, it is actually the full path of the node that is recorded when the node is created. The following figure is an example.

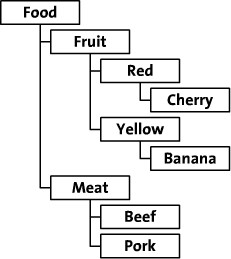
The result of storing according to Path Enumeration is as follows.

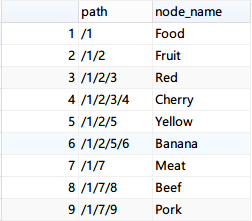
This solution is based on the idea of unix file directories, and mainly trades space for time.

Query all the children nodes under a certain node: (Take Fruit as an example)

1
2

SET @path = (SELECT path FROM pathTree WHERE node_name = 'Fruit');
SELECT * FROM pathTree WHERE path like CONCAT(@path,'/%');

How to query direct child nodes? MySQL regular expression query is needed for.

1
2

SET @path = (SELECT path FROM pathTree WHERE node_name = 'Fruit');
SELECT * FROM pathTree WHERE path REGEXP CONCAT(@path,'/','[0-9]$');

Query all superiors of any node: (take Yellow as an example).

1
2

SET @path = (SELECT path FROM pathTree WHERE node_name = 'Yellow');
SELECT * FROM pathTree WHERE @path LIKE CONCAT(path, '%') AND path <> @path;

Insert additional data.

1
2

SET @parent_path = ( SELECT path FROM pathTree WHERE node_name = 'Fruit');
INSERT INTO pathtree (path,node_name) VALUES (CONCAT(@parent_path,'/',LAST_INSERT_ID()+1),'White')

The disadvantage of this scheme is that the depth of the tree may exceed the length of the PATH field, so the maximum depth it can support is not infinite.

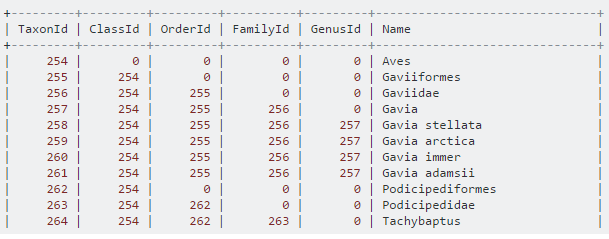
If the number of hierarchies is determined, all columns can be expanded again, as shown below, which is more tried for content with determined hierarchies like administrative divisions, biological taxonomy (boundary, phylum, order, family, genus, species).

Closure Table

Closure Table is a more thorough full path structure that records the full expansion form of related nodes on the path respectively. It can clarify the relationship between any two nodes without redundant queries, and cascade deletion and node movement are also very convenient. But its storage overhead will be larger, in addition to the Meta information of the nodes, but also need a special relationship table.

The following diagram gives an example of data example.

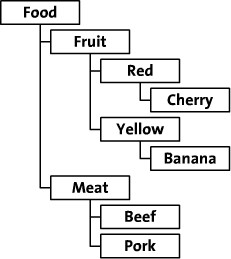
Create master table.

1
2
3
4
5

CREATE TABLE nodeInfo (
    node_id INT NOT NULL AUTO_INCREMENT,
    node_name VARCHAR (255),
    PRIMARY KEY (`node_id`)
) DEFAULT CHARSET = utf8;

Create relationship tables.

1
2
3
4
5
6

CREATE TABLE nodeRelationship (
    ancestor INT NOT NULL,
    descendant INT NOT NULL,
    distance INT NOT NULL,
    PRIMARY KEY (ancestor, descendant)
) DEFAULT CHARSET = utf8;

where

  • Ancestor represents an ancestor node
  • Descendant represents the descendant node
  • Distance Ancestor is the distance from Descendant

Adding data (creating a stored procedure)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

CREATE DEFINER = `root`@`localhost` PROCEDURE `AddNode`(`_parent_name` varchar(255),`_node_name` varchar(255))
BEGIN
    DECLARE _ancestor INT;
    DECLARE _descendant INT;
    DECLARE _parent INT;
    IF NOT EXISTS(SELECT node_id From nodeinfo WHERE node_name = _node_name)
    THEN
        INSERT INTO nodeinfo (node_name) VALUES(_node_name);
        SET _descendant = (SELECT node_id FROM nodeinfo WHERE node_name = _node_name);
        INSERT INTO noderelationship (ancestor,descendant,distance) VALUES(_descendant,_descendant,0);
        IF EXISTS (SELECT node_id FROM nodeinfo WHERE node_name = _parent_name)
        THEN
            SET _parent = (SELECT node_id FROM nodeinfo WHERE node_name = _parent_name);
            INSERT INTO noderelationship (ancestor,descendant,distance) SELECT ancestor,_descendant,distance+1 from noderelationship where descendant = _parent;
        END IF;
    END IF;
END;

The data in the 2 tables after completion looks roughly like this: (Note: each node has a record to itself.)

Query all child nodes under Fruit.

1
2
3
4
5
6
7
8
9

SELECT
    n3.node_name
FROM
    nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor
INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id
WHERE
    n1.node_name = 'Fruit'
AND n2.distance != 0

Query the direct child nodes under Fruit.

1
2
3
4
5
6
7
8
9

SELECT
    n3.node_name
FROM
    nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor
INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id
WHERE
    n1.node_name = 'Fruit'
AND n2.distance = 1

Query the tier that Fruit is in.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

SELECT
    n2.*, n3.node_name
FROM
    nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.descendant
INNER JOIN nodeinfo n3 ON n2.ancestor = n3.node_id
WHERE
    n1.node_name = 'Fruit'
ORDER BY
    n2.distance DESC

It is also very simple to delete nodes, so I will not elaborate much here.

Left and Right Value Coding Nested Set

In general database based applications, the need for queries is always greater than that for deletions and modifications. In order to avoid the “recursive” process of querying a tree structure, we design a new non-recursive querying, infinitely grouped left and right value encoding scheme based on Tree’s preorder traversal to save the data of the tree.

The first time you see this table structure, I believe most people are not sure how the left value (Lft) and right value (Rgt) are calculated, and this table design does not seem to preserve the inheritance relationship between parent and child nodes. But when you point your finger at the numbers in the table and count from 1 to 18, you should find something, right? Yes, the order in which you move your finger is the order in which the tree is traversed in preorder, as shown in the figure below. When we start from the left side of the root node Food, marked as 1, and along the direction of the traversal of the previous order, in order to mark the numbers on the traversal path, we finally came back to the root node Food, and wrote 18 on the right side.

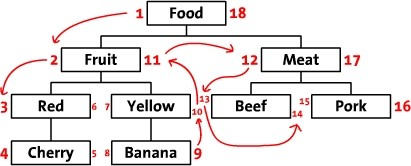
Based on this design, we can infer that all nodes with left values greater than 2 and right values less than 11 are the successor nodes of Fruit, and the structure of the whole tree is stored by the left and right values. However, this is not enough, our aim is to be able to perform CRUD operations on the tree, i.e., we need to construct the relevant algorithm to go with it. The tree is traversed in depth-first, left-to-right order, and each node is labeled with a left value and a right value starting from 1, and these two values are stored in the corresponding name.

How to query?

  1. Get all the children nodes under a node, take Fruit as an example.
1

SELECT * FROM Tree WHERE Lft > 2 AND Lft < 11 ORDER BY Lft ASC
  1. Get the total number of descendant nodes

Total number of children = (right value - left value - 1)/2, take Fruit as an example, its total number of children is: (11-2-1)/2 = 4

  1. Get the number of levels the node is at in the tree, taking Fruit as an example.
1

SELECT COUNT(*) FROM Tree WHERE Lft <= 2 AND Rgt >=11
  1. Get the path where the current node is located, taking Fruit as an example.
1

SELECT * FROM Tree WHERE Lft <= 2 AND Rgt >=11 ORDER BY Lft ASC

In our daily processing we often also encounter the need to obtain the immediate superior, sibling, or immediate subordinate of a node. To better describe the hierarchical relationship, we can create a view for Tree, adding a hierarchical column whose value can be calculated by writing a custom function.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

CREATE FUNCTION `CountLayer`(`_node_id` int)
 RETURNS int(11)
BEGIN
    DECLARE _result INT;
    DECLARE _lft INT;
    DECLARE _rgt INT;
    IF EXISTS(SELECT Node_id FROM Tree WHERE Node_id = _node_id)
    THEN
        SELECT Lft,Rgt FROM Tree WHERE Node_id = _node_id INTO _lft,_rgt;
        SET _result = (SELECT COUNT(1) FROM Tree WHERE Lft <= _lft AND Rgt >= _rgt);    
        RETURN _result;
    ELSE
        RETURN 0;
    END IF;
END;

After adding the function, we create an a-view and add the new hierarchical column.

1
2

CREATE VIEW `NewView`AS 
SELECT Node_id, Name, Lft, Rgt, CountLayer(Node_id) AS Layer FROM Tree ORDER BY Lft ;
  1. Get the parent node of the current node, using Fruit as an example.
1

SELECT * FROM treeview WHERE Lft <= 2 AND Rgt >=11 AND Layer=1
  1. Get all direct child nodes, taking Fruit as an example.
1

SELECT * FROM treeview WHERE Lft BETWEEN 2 AND 11 AND Layer=3
  1. Get all sibling nodes, using Fruit as an example.
1

SELECT * FROM treeview WHERE Rgt > 11 AND Rgt < (SELECT Rgt FROM treeview WHERE Lft <= 2 AND Rgt >=11 AND Layer=1) AND Layer=2
  1. Return all leaf nodes
1

SELECT * FROM Tree WHERE Rgt = Lft + 1

How to create a tree? How to add data?

The above has described how to retrieve the results, so how can we add new nodes?

The most important thing about Nested set is that there must be a root node as the starting point of all nodes, and usually this node is not used. In order to control the query level, it is recommended to add the parent_id when building the table together with the linked list method.

1
2
3
4
5
6
7
8
9

CREATE TABLE IF NOT EXISTS `Tree` (
  `node_id` int(11) NOT NULL AUTO_INCREMENT,
  `parent_id` int(10) UNSIGNED NOT NULL DEFAULT '0',
  `name` varchar(255) NOT NULL,
  `lft` int(11) NOT NULL DEFAULT '0',
  `rgt` int(11) NOT NULL DEFAULT '0',
  PRIMARY KEY (`node_id`),
  KEY `idx_left_right` (`lft`,`rgt`)
) DEFAULT CHARSET=utf8;

1

INSERT INTO `Tree` (parent_id,name,lft,rgt) VALUES ( 0,'Food',1,2)

Add a child node (at the start of the child node). Take the example of adding a child node Fruit under Food.

1
2
3
4
5
6

LOCK TABLE Tree WRITE;
SELECT @parent_id := node_id, @myLeft := lft FROM Tree WHERE name = 'Food';
UPDATE Tree SET rgt = rgt + 2 WHERE rgt > @myLeft;
UPDATE Tree SET lft = lft + 2 WHERE lft > @myLeft;
INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Fruit', @myLeft + 1, @myLeft + 2);
UNLOCK TABLES;

If you need to append at the end, you need to do the following (for example, add Apple under Red).

1
2
3
4
5
6

LOCK TABLE Tree WRITE;
SELECT @parent_id := node_id , @myRight := rgt FROM Tree WHERE name = 'Red';
UPDATE Tree SET rgt = rgt + 2 WHERE rgt >= @myRight;
UPDATE Tree SET lft = lft + 2 WHERE lft > @myRight;
INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Apple', @myRight, @myRight + 1);
UNLOCK TABLES;

Add a sibling node after node A (for example, add Green after Yellow)

1
2
3
4
5
6

LOCK TABLE Tree WRITE;
SELECT @parent_id := parent_id , @myRight := rgt FROM Tree WHERE name = 'Yellow';
UPDATE Tree SET rgt = rgt + 2 WHERE rgt > @myRight;
UPDATE Tree SET lft = lft + 2 WHERE lft > @myRight;
INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Green', @myRight+1, @myRight+2);
UNLOCK TABLES;

The above discussion of adding nodes refers to adding end nodes, i.e., the node inserted is not the parent node of the currently existing node. What should we do if we need to insert a non-end node?

The process can be divided into 2 steps: first add a new node, and then move the required node to the lower level of the new node. Node movement method (for example, moving Apple to Yellow).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

LOCK TABLE Tree WRITE;
SELECT @nodeId := node_id , @myLeft := lft , @myRight := rgt FROM Tree WHERE name = 'Apple';
UPDATE Tree SET lft = lft - (@myRight - @myLeft) - 1 WHERE lft > @myRight;
UPDATE Tree SET rgt = rgt - (@myRight - @myLeft) - 1 WHERE rgt > @myRight;
SELECT @parent_id := node_id , @Left := lft , @Right := rgt FROM Tree WHERE name = 'Yellow';
UPDATE Tree SET lft = lft + (@myRight - @myLeft) + 1 WHERE lft > @Left;
UPDATE Tree SET rgt = rgt + (@myRight - @myLeft) + 1 WHERE lft > @Left;
UPDATE Tree SET parent_id = @parent_id WHERE name = node_id = @nodeId;
UPDATE Tree SET lft = @Left + lft - @myLeft + 1, rgt = @Left + lft - @myLeft + 1  + (@myRight - @myLeft) WHERE lft >= @myLeft AND rgt <= @myRight;
UNLOCK TABLES;

delete nodes (including child nodes)

1
2
3
4
5
6

LOCK TABLE Tree WRITE;
SELECT @myLeft := lft , @myRight := rgt FROM Tree WHERE name = 'Apple';
DELETE Tree WHERE lft >= @myLeft AND rgt <= @myRight;
UPDATE Tree SET lft = lft - (@myRight - @myLeft) - 1 WHERE lft > @myRight;
UPDATE Tree SET rgt = rgt - (@myRight - @myLeft) - 1 WHERE rgt > @myRight;
UNLOCK TABLES;

What if I need to delete only that node and the child nodes are automatically moved up one level?

1
2
3
4
5
6
7

LOCK TABLE Tree WRITE;
SELECT @parent_id := parent_id , @node_id :=node_id , @myLeft := lft , @myRight := rgt FROM Tree WHERE name = 'Red';
UPDATE Tree SET parent_id = @parent_id WHERE  parent_id = @node_id
DELETE Tree WHERE lft = @myLeft;
UPDATE Tree SET lft = lft - 1,rgt = rgt-1 Where lft > @myLeft AND @rgt < @myRight
UPDATE Tree SET lft = lft - 2,rgt = rgt-2 Where lft > @rgt > @myRight
UNLOCK TABLES;

The above is the CURD operation of Nested Set, specifically in the use of the recommended combination of transactions and stored procedures together. The advantage of this solution is that it is very convenient to query, but the disadvantage is that each insertion and deletion of data involves too many updates, and if the tree is very large, it may take a long time to insert a piece of data.

interval nested Nested Intervals

The previous introduced the left and right value encoding, I wonder if you have noticed that if the data is huge, each update needs to update almost the entire table, less efficient no better way? Today we will study the interval nesting method.

interval nesting method principle

If the node interval [clft, crgt] and [plft, prgt] have the following relationship: plft <= clft and crgt >= prgt, then the points in the interval [clft, crgt] are the children of [plft, prgt]. Based on this assumption, we can obtain new intervals by continuously scribing down the interval. For example, if there is a blank interval [lft1, rgt1] in the interval [plft, prgt], to add an interval of the same level as [plft,lft1], [rgt1,prgt], just insert the nodes: [(2lft1+rgt1)/3, (rgt1+2lft)/3]. After adding the nodes we are left with [lft1,(2lft1+rgt1)/3] and [(rgt1+2lft)/3,rgt1] two free spaces to add more child nodes.

If we put the intervals in the two-bit plane and treat rgt as the x-axis and lft as the y-axis, then the number of nested intervals is almost like this

Each node [lft, rgt] has children that are contained in y >= lft & x <= rgt. Also the space where y >= clft & x <= crgt is located is a subset of y >= plft & x <= prgt. In addition, since the new right intervals are smaller than the existing left intervals, the new nodes are below the line y = x.

Interval nesting method implementation

After understanding the principle of the interval nesting method, we will consider how to implement it, in principle, the initial interval can use any interval, here we use [0,1] as the root interval.

First, we define 2 points in the XY plane. Depth-first set point and breadth-finite set point for the point <x=1,y=1/2> with depth-first set point <x=1,y=1> and breadth-first set point <x=1/2,y=1/2>. Next, we define the position of the first child node as the midpoint between the parent node and the depth-first set point. The sibling node is the midpoint from the previous child node to the breadth-first set point, as shown in the figure above, where node 1.2 is at <x=3/4, y=5/8>.

Also looking closely we can see the relationship between the points. Also if we know the sum of x and y, we can invert the value of x,y (what is the exact logic, I haven’t figured it out yet either, any of you who know can help explain).

Let’s take the node <x=3/4, y=5/8> as an example, we can get his sum to 11/8.

We define 11 as the numerator (numerator) and 8 as the denominator (denominator), then the numerator of point x is

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

CREATE DEFINER = `root`@`localhost` FUNCTION `x_numer`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE ret_num INT;
    DECLARE ret_den INT;
    SET ret_num := numer+1;
    SET ret_den := denom*2;
    WHILE floor(ret_num/2) = ret_num/2 DO
        SET ret_num := ret_num/2;
        SET ret_den := ret_den/2;
    END WHILE;
    RETURN ret_num;
END;

The denominator of point x is.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

CREATE DEFINER = `root`@`localhost` FUNCTION `x_ denom`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE ret_num INT;
    DECLARE ret_den INT;
    SET ret_num := numer+1;
    SET ret_den := denom*2;
    WHILE floor(ret_num/2) = ret_num/2 DO
        SET ret_num := ret_num/2;
        SET ret_den := ret_den/2;
    END WHILE;
    RETURN ret_den;
END;

Molecules at point Y.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

CREATE DEFINER = `root`@`localhost` FUNCTION `y_numer`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE num INT;
    DECLARE den INT;
    SET num := x_numer(numer, denom);
    SET den := x_denom(numer, denom);
    WHILE den < denom DO
        SET num := num*2;
        SET den := den*2;
    END WHILE;
    SET num := (numer - num);
    WHILE floor(num/2) = num/2 DO
        SET num := num/2;
        SET den := den/2;
    END WHILE;
    RETURN num;
END;

Denominator of Y.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

CREATE DEFINER = `root`@`localhost` FUNCTION `y_denom`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE num INT;
    DECLARE den INT;
    SET num := x_numer(numer, denom);
    SET den := x_denom(numer, denom);
    WHILE den < denom DO
        SET num := num*2;
        SET den := den*2;
    END WHILE;
    SET num := (numer - num);
    WHILE floor(num/2) = num/2 DO
        SET num := num/2;
        SET den := den/2;
    END WHILE;
    RETURN den;
END;

Next, let’s test whether X and Y can be decoded.

1
2
3

SELECT
    CONCAT(x_numer (11, 8),'/',x_denom (11, 8)) AS X,
    CONCAT(y_numer (11, 8),'/',y_denom (11, 8)) AS Y

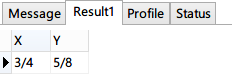
The result is identical to the position of node 1.2 as <x=3/4, y=5/8>. Now we know that only one fraction is needed to represent a point on the plane.

If there is already a fraction 11/8 how do we get the parent of that node? (If the numerator is 3, it means it is the root node)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

CREATE DEFINER = `root`@`localhost` FUNCTION `parent_numer`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE ret_num INT;
    DECLARE ret_den INT;
    IF numer=3 THEN
        RETURN denom/2;
    END IF;
    SET ret_num := (numer-1)/2;
    SET ret_den := denom/2;
    WHILE floor((ret_num-1)/4) = (ret_num-1)/4 DO
        SET ret_num := (ret_num+1)/2;
        SET ret_den := ret_den/2;
    END WHILE;
    RETURN ret_num;
END;

1

SELECT CONCAT(parent_numer(11,8),'/',parent_denom(11,8)) AS parent

Calculate the position of the current node at the sibling level.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

CREATE DEFINER = `root`@`localhost` FUNCTION `parent_denom`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE ret_num INT;
    DECLARE ret_den INT;
    IF numer=3 THEN
        RETURN NULL;
    END IF;
    SET ret_num := (numer-1)/2;
    SET ret_den := denom/2;
    WHILE floor((ret_num-1)/4) = (ret_num-1)/4 DO
        SET ret_num := (ret_num+1)/2;
        SET ret_den := ret_den/2;
    END WHILE;
    RETURN ret_den;
END;

With the method of querying the parent node and the position of the current node in the same level, the path of the node can be calculated by the combination of these two methods.

1
2
3
4
5
6
7
8

CREATE DEFINER = `root`@`localhost` FUNCTION `path`(`numer` int,`denom` int)
 RETURNS varchar(255)
BEGIN
    IF numer is NULL THEN
        RETURN '';
    END IF;
    RETURN path(parent_numer(numer, denom),parent_denom(numer, denom))|| ‘.’ || sibling_number(numer, denom);
END;

After adding the above method and testing, it returns [Err] 1424 - Recursive stored functions and triggers are not allowed. That is, MySQL’s custom functions do not support recursive queries.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

CREATE DEFINER = `root`@`localhost` FUNCTION `path`(`numer` int,`denom` int)
 RETURNS varchar(255)
BEGIN
    DECLARE numer_temp INT;
    DECLARE denom_temp INT;
    DECLARE path_result VARCHAR(255);
    DECLARE path_temp VARCHAR(255);
    DECLARE sn VARCHAR(255);
    SET path_temp := '';
    WHILE numer IS NOT NULL DO
        IF path_temp = ''
        THEN
            SET path_result := sibling_number(numer, denom);
        ELSE
            SET path_result := CONCAT(sibling_number(numer, denom),'.',path_temp);
        END IF;
        SET path_temp := path_result;
        SET numer_temp := parent_numer(numer, denom);
        SET denom_temp := parent_denom(numer, denom);
        SET numer := numer_temp;
        SET denom := denom_temp;
    END WHILE;
    RETURN path_result;
END;

The result of SELECT path (11, 8) is 1.2

Calculate the node hierarchy by

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

CREATE DEFINER = `root`@`localhost` FUNCTION `node_level`(`numer` int,`denom` int)
 RETURNS int(11)
BEGIN
    DECLARE ret_num INT;
    DECLARE ret_den INT;
    DECLARE ret INT;
    SET ret =1;
    IF numer=3 THEN
        return 1;
    END IF;
    WHILE numer!=3 DO
        SET ret_num := parent_numer(numer, denom);
        SET ret_den := parent_denom(numer, denom);
        SET numer := ret_num;
        SET denom := ret_den;
        SET ret := ret + 1;
    END WHILE;
    RETURN ret;
END;

We know how to convert the encoded nodes into directory form, how to reverse it? The following is the method.

First add 2 helper functions.

1
2
3
4
5

CREATE DEFINER = `root`@`localhost` FUNCTION `child_numer`(`num` int,`den` int,`child` int)
 RETURNS int(11)
BEGIN
    RETURN num * power(2, child) + 3 - power(2, child);
END;

1
2
3
4
5

CREATE DEFINER = `root`@`localhost` FUNCTION `child_denom`(`num` int,`den` int,`child` int)
 RETURNS int(11)
BEGIN
    RETURN den*power(2, child);
END;

To write the reversal function again.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

CREATE DEFINER = `root`@`localhost` FUNCTION `path_numer`(`path` varchar(255))
 RETURNS int(11)
BEGIN
    DECLARE num INT;
    DECLARE den INT;
    DECLARE postfix VARCHAR(255);
    DECLARE sibling VARCHAR(255);
    SET num := 1;
    SET den := 1;
    SET postfix := CONCAT(path,'.');
    WHILE length(postfix) > 1 DO
        SET sibling := SUBSTR(postfix, 1, instr(postfix,'.')-1);
        SET postfix := SUBSTR(postfix, instr(postfix,'.')+1);
        SET num := child_numer(num,den,sibling+0);
        SET den := child_denom(num,den,sibling+0);
    END WHILE;
    RETURN num;
END;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

CREATE DEFINER = `root`@`localhost` FUNCTION `path_denom`(`path` varchar(255))
 RETURNS int(11)
BEGIN
    DECLARE num INT;
    DECLARE den INT;
    DECLARE postfix VARCHAR(255);
    DECLARE sibling VARCHAR(255);
    SET num := 1;
    SET den := 1;
    SET postfix := CONCAT(path,'.');
    WHILE length(postfix) > 1 DO
        SET sibling := SUBSTR(postfix, 1, instr(postfix,'.')-1);
        SET postfix := SUBSTR(postfix, instr(postfix,'.')+1);
        SET num := child_numer(num,den,sibling+0);
        SET den := child_denom(num,den,sibling+0);
    END WHILE;
    RETURN den;
END;

select CONCAT(path_numer(‘2.1.3′),’/’,path_denom(‘2.1.3’)) The result is 51/64

Reference link.